Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

2) Воздух давит? на открытую внешнюю часть дамбы. Это давление прибавляется также к давлению воды на внутреннюю поверхность дамбы.

Таким образом, при определении сил, опрокидывающих дамбу, эти два давления компенсируются. Поэтому в приведенных вычислениях атмосферным давлением можно пренебречь. Вычислите:

а) давление на открытой поверхности воды (ответ: нуль);

б) давление на дне водоема;

в) среднее давление на участке от верхнего уровня воды до дна (руководствуйтесь здравым смыслом);

е) общую силу, с которой вода давит на дамбу.

[ Указание : (давление) = (сила)/(площадь); (сила) = (давление)∙(площадь). Для расчета силы используйте среднее давление.]

Задача 5 (трудная)

Дамба построена слишком низкой, так что уровень воды оказался на 60 см выше верхнего края дамбы и вода переливается через дамбу (фиг. 86). Ширина дамбы 30 м, высота 12 м, а высота воды за дамбой 12,16 м. Следуя ходу вычислений задачи 4 , найдите общую силу, действующую на эту дамбу. (Пренебрегите всеми незнакомыми вам изменениями давления, обусловленными быстрым движением воды, например «эффектом Бернулли».)

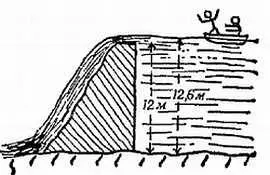
Фиг. 86. К задаче 5.

Законы давления (согласно Паскалю )

В покоящейся жидкости [53] Если жидкость движется, то нужно учитывать дополнительные факторы, например трение и «эффекты Бернулли» (см. гл. 9 ). давление подчиняется следующим правилам.

I. Давление одинаково по всему дну прямоугольного сосуда с жидкостью. В более общей форме давление одинаково во всех точках, которые находятся на одном и том же уровне в одной и той же жидкости (или газе).

II. Давление жидкости на любую поверхность направлено перпендикулярно к ней. (Водолаз, который держит в руке монету, убеждается, что независимо от того, как повернута монета, давление оказывается перпендикулярным к ее поверхности.)

III. В любой точке жидкости давление действует одинаково во всех направлениях. (Водолаз, который держит в руке монету, убеждается, что давление на монету одинаково независимо от того, в какую сторону она повернута.)

IV. Давление передается без потерь внутри жидкости из одного места в другое. (Если надавить на поршень гидравлической системы, то созданное давление передается на каждую стенку и на каждый другой поршень в системе.)

V. Разность давлений между любыми двумя точками в жидкости равна произведению h ∙ d , где h — разность уровней по вертикали, и d — плотность жидкости. На этом основан простой способ измерения давлений, который описан ниже.

Алгебраический вывод I и V законов давления

Закон I. Давление одинаково по всему дну прямоугольного сосуда с жидкостью. Давление на любой участок дна можно рассчитать следующим образом.

Выберем участок площадью А см 2.

Найдем вес вертикального столба жидкости, который опирается на основание А , т. е. силу притяжения, которая действует на эту часть жидкости (фиг. 87). Затем, чтобы найти давление, разделим этот вес на площадь основания А :

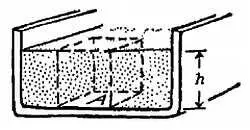
Фиг. 87. Закон I.Давление одинаково по всему дну прямоугольного бака с жидкостью.

ОБЪЕМ СТОЛБА = ВЫСОТА ∙ ПЛОЩАДЬ = h∙ А,

МАССА ЖИДКОСТИ В ЭТОМ СТОЛБЕ = ОБЪЕМ ∙ (МАССА / ОБЪЕМ) = ОБЪЕМ ∙ ПЛОТНОСТЬ = hА∙ d.

При применении «плохих» единиц (таких, как кГ) масса столба жидкости, выраженная в кг, численно равна весу жидкости в единицах кГ. Таким образом,

ДАВЛЕНИЕ р= СИЛА / ПЛОЩАДЬ = ВЕС СТОЛБА / ПЛОЩАДЬ ОСНОВАНИЯ = hAd/ A= hd

Итак, давление на любую площадь основания равно произведению

ГЛУБИНА ЖИДКОСТИ ∙ ПЛОТНОСТЬ

и не зависит от размера площади .

Если мы хотим выразить вес в «хороших» единицах, например в ньютонах, то должны умножить массу на ускорение силы тяжести g (9,8 ньютон/кг). Тогда

ДАВЛЕНИЕ = h∙ d∙(УСКОРЕНИЕ СИЛЫ ТЯЖЕСТИ g),

ДАВЛЕНИЕ НА ЛЮБУЮ ПЛОЩАДЬ ДНА = ГЛУБИНА ЖИДКОСТИ ∙ ПЛОТНОСТЬ . g.

Закон V. Разность давлений между двумя точками в жидкости равна

Δ (ВЫСОТА) ∙ ПЛОТНОСТЬ.

Чтобы найти разность давлений ( P Y— Р Х) между точками Y и Х , выделим в жидкости прямоугольный объем или вертикальный столб с площадью основания А и высотой h от Y до X (фиг. 88).

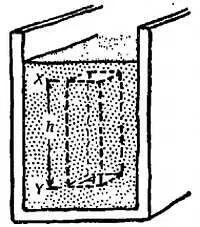
Фиг. 88. Закон V.Разность давлений между двумя точками в жидкости равна Δ (Высота)∙Плотность.

Этот участок жидкости находится в равновесии, поэтому равнодействующая всех вертикальных сил, действующих на него, должна быть равна нулю. На этот участок жидкости действуют силы:

Вес жидкости в столбе , h∙ A∙ d;

Направленное вниз давление окружающей жидкости на вершину,

P х∙ А;

Направленное вверх давление окружающей жидкости на основание,

P Y∙ А.

Отсюда

P Y∙ А = P х∙ А+ h∙ A∙ d,

P Y — P х= h∙ d.

В «хороших» (абсолютных) единицах

P Y — P х= h∙ d∙ g

Измерение разности давления с помощью U-образных манометров

Для измерения давлений часто используют заполненные жидкостью U-образные трубки, которые не обязательно должны иметь колена одинакового размера. Их действие основано на только что выведенной формуле

РАЗНОСТЬ ДАВЛЕНИЙ = h∙ d.

Например, надо измерить давление р , которое создается дыханием человека (фиг. 89).

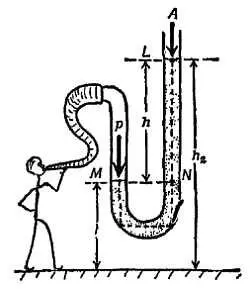
Фиг. 89. Измерение давления.

Итак, давление в точке М равно р . Давление в точке N , противоположной М , также равно р (чтобы убедиться в этом, можно проследить переход от точки М вниз до дна, затем поперек соединительного колена и потом вверх к точке N ). В точке L давление равно атмосферному, А . Но

(ДАВЛЕНИЕ В N ) = (ДАВЛЕНИЕ В L ) + ( h∙ d);

т. е.

ДАВЛЕНИЕ p= A+ h∙ d.

Единицы давления

С помощью формулы p= h∙ dполучают разность давлений в «инженерных единицах», например в кг/м 2. (Строго говоря, применяемую здесь единицу силы надо называть килограмм∙сила.)