Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

УДЛИНЕНИЕ ~ НАГРУЗКА [или (НАГРУЗКА)/(УДЛИНЕНИЕ) = соnst ],

мы получаем более обобщенное отношение, которое, подобно отношению (нагрузка)/(удлинение), постоянно. Но это обобщенное отношение не зависит ни от формы, ни от размера используемого образца. Оно одинаково для всех образцов данного материала. Чтобы вывести обобщеннов отношение, мы используем напряжение и деформацию вместо нагрузки и удлинения. Теперь мы можем представить закон Гуна в общей, итоговой форме:

?/? = const

Эта постоянная называется модулем. Чем легче вещество растягивается (или сжимается), тем

___________ должен быть его модуль.

(больше?/меньше?)

Используя напряжение и деформацию, можно представить закон Гука в общей форме: ( напряжение )/( деформация ) = const ; это значит, что отношение

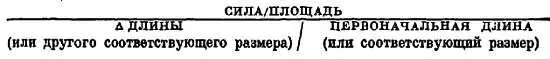
постоянно.

Такое отношение ( напряжение )/( деформация ) мы называем модулем .

В пределах справедливости закона Гука модуль является характеристикой материала, различной для различных видов деформации, но не зависящей ни от формы, ни от размеров образца и приложенной силы. Чем больше сила, необходимая для придания материалу заданной деформации, тем больше модуль. Следовательно, величина модуля характеризует жесткость материала, а не легкость его растяжения и т. п.

Для чистого растяжения стержня или проволоки с помощью растягивающей силы (мы об этом говорили) модуль, определяемый отношением ( напряжение )/( деформация ), называется модулем Юнга (модуль продольной упругости). Он относится также и к сжатию (фиг. 104, а ). Инженеры пользуются им, чтобы заранее определять возможные изменения мостовых балок при их растяжении или сжатии.

При изгибе упругой балки одни волокна растягиваются, другие сжимаются (фиг. 104, б ), поэтому модуль Юнга применяется и при изгибе. Пометьте резиновую трубку или резиновый брусок чернилами и постарайтесь растянуть или изогнуть их.

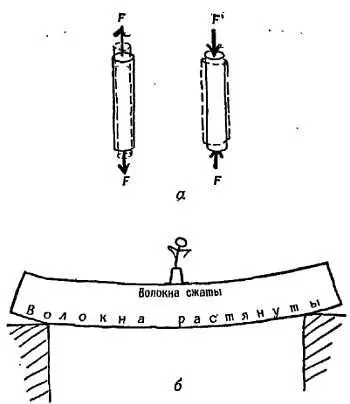
Фиг. 104. Растяжение (сжатие) стержня или проволоки ( а) и изгиб балки ( б).

Сильнее сжимаются и растягиваются внешние волокна, поэтому в них возникают большие давления и напряжения, препятствующие изгибу. Внутренние волокна претерпевают малые деформации, и, следовательно, в них возникают малые силы. Их можно удалить с небольшой потерей прочности, но с весьма существенной экономией в весе. Именно поэтому сплошные балки заменяются двутавровыми (I-образными, фиг. 105), а в велосипедных рамах ставят не сплошные, а пустотелые детали трубчатой формы.

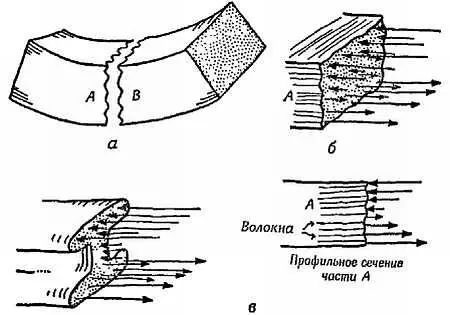
Фиг. 105. Изогнутая балка.

а— балка разрезана на части А и В; б— волокна части В создают силы, приложенные к части А; в— двутавровая балка может быть намного легче, но обладает той же прочностью при изгибе.

Для других видов деформации существуют другие модули.

Для чистого изменения размера без изменения формы (т. е. чистого сжатия, фиг. 106) применяется объемный модуль .

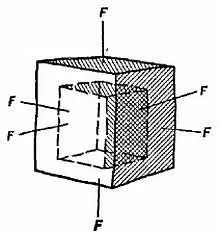
Фиг. 106. Чистое изменение размеров.

Сжимающее напряжение легко осуществляется с помощью давления жидкости.

Для чистого изменения формы без изменения размеров (сдвиг) существует модуль сдвига . При кручении стержня происходит сдвиг, поэтому здесь применяется модуль сдвига. Попробуйте скрутить резиновый брусок или трубку, помеченные чернилами.

Положите толстую книгу на стол и толкайте переплет так, чтобы страницы скользили одна по другой. Начерченный карандашом на обрезе книги прямоугольник деформируется и приобретает форму ромба (фиг. 107 и 108).

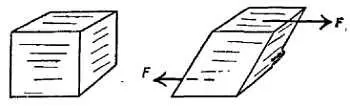
Фиг. 107. Сдвиг.

При сдвиге квадратные стороны кубического блока принимают форму ромба.

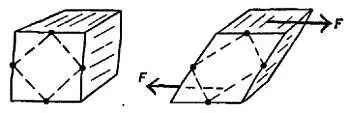
Фиг. 108. Другой пример деформации сдвига.

Наклонные волокна блока растягиваются и сжимаются так, что его стороны из ромбов с острыми углами 45° становятся прямоугольниками. Попытайтесь проделать это с блоком большой книги.

В книге происходит сдвиг; ее форма изменяется, но объем остается прежним. Вы можете вообразить, что каждый слой атомов или молекул (каждая страница книги) принужден скользить поверх следующего слоя, испытывая возрастающую сдерживающую силу. Когда стержень закручивается, волокна, первоначально параллельные оси стержня, отклоняются от нее и оказываются сдвинутыми (фиг. 109).

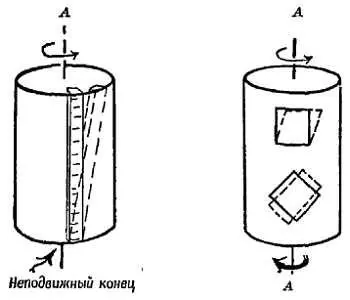
Фиг. 109. Закручивание цилиндра.

Волокно сдвигается и занимает наклонное положение, а квадраты, начерченные на поверхности цилиндра, иллюстрируют деформацию сдвигом. А — закрученный конец.

Внутренние слои скрученного стержня претерпевают относительно малые деформации, создают малые противодействующие напряжения и, следовательно, мало участвуют в сопротивлении стержня скручиванию. Трубка почти так же прочна, как сплошной стержень, но намного легче.

Деформации в различных материалах

Жидкости и газы не оказывают постоянного сопротивления изменению формы, и, таким образом, модуль сдвига к ним неприменим. Но при изменении объема они проявляют упругие свойства, которые характеризуются объемным модулем сжатия. Жидкости подчиняются закону Гука, объем их изменяется в пределах большого диапазона давлений; газы легко отклоняются от закона Гука, и для них должен быть найден другой закон. Для твердых тел простые изменения сдвига и сжатия могут комбинироваться с более сложными видами деформаций, например в спиральных пружинах или в подъемно-транспортных машинах, и во всех случаях обычного поведения материалов по закону Гука отношение

НАПРЯЖЕНИЕ (соответствующее приложенным силам)/ДЕФОРМАЦИЯ (искажение)

выдерживается в широком диапазоне постоянным для данного материала; иначе говоря, ( напряжение )~( деформация ),

Закон Гука

Общая форма закона Гука

НАПРЯЖЕНИЕ/ДЕФОРМАЦИЯ = const

приложима ко всем материалам (в известных пределах) и ко многим видам деформации. Закон замечателен и полезен не только потому, что прост, но и вследствие широкого диапазона применения. Спиральная стальная пружина с плотно прилегающими витками может растягиваться до длины, в 5 или 10 раз превышающей первоначальную, прежде чем достигнет своего предела пропорциональности.