Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Мыльные пленки. Поверхностные свойства жидкостей удобно наблюдать на мыльных пузырях и пленках, которые «состоят только из поверхности и не имеют внутренности» и вес которых слишком мал, чтобы он мог противостоять поверхностным силам. На фиг. 111 схематически изображены соответствующие опыты.

Опыт 7.Мыльный пузырь на воронке сжимается, задувая пламя свечи (фиг. 111, а ).

Опыт 8.«Оконная штора». На проволочной рамке, нижний край которой подвижен, создается мыльная пленка. Ее растягивают, спуская за нить скользящую часть шторы вниз, а затем нить отпускают (фиг. 111, б ).

Опыт 9.На квадратной проволочной рамке создают мыльную пленку. На пленку кладут шелковую нить, связанную в виде небольшой петли (фиг. 114, в ). Затем пленку внутри петли разрывают.

Опыт 10.Опыт «оконная штора» повторяют с помощью рамки, имеющей подвижные стержни сверху и снизу (фиг. 111, г ). Верхний стержень удерживается небольшой пружиной. Мыльная пленка создается между двумя стержнями, после чего нижний стержень двигают с помощью нити вверх и вниз.

Опыт 11.На концах Т-образной трубки выдувают два мыльных пузыря разного размера (фиг. 111, д ). Затем конец, через который производили выдувание, закрывают, и оба пузыря остаются соединенными.

Фиг. 111. Мыльные пузыри.

Задача 2

Запишите ваши наблюдения о каждом из описанных опытов, а затем скажите, какие выводя можно сделать из них относительно мыльных пленок и их «поверхностного натяжения». ( Замечание . Плоская фигура с максимальной площадью при заданном периметре есть круг.) Предупреждение . Важное следствие из опыта 8 исключает простейшее объяснение опыта 11 .

Общие пояснения

Что говорят эти опыты о поверхностях жидкостей? Капли, образующиеся в водопроводном кране, выглядят так, как будто они заключены в резиновый мешок.

Взяв настоящую оболочку из тонкой резины, мы можем сделать большую искусственную «каплю», которая по мере того, как внутрь оболочки будет вливаться все больше воды, примет форму реальной капли; однако возрастающее натяжение резины помешает точной аналогии.

Капли дождя и лужицы жидкости на столе, по-видимому, стремятся принять круглую форму, что также наводит на мысль об оболочке, которая сжимает их и противодействует силе тяжести.

Обдумав эти наблюдения, можно сделать два вывода, расплывчатых и рискованных, но заслуживающих дальнейшей проверки.

А . Поверхности жидкостей ведут себя так, будто их удерживает эластичная оболочка, стремящаяся придать им круглую форму.

Б . «Эффект оболочки» более заметен при малых размерах (маленькие капли), чем при больших (лужи воды), но когда сила тяжести уравновешена другими силами, он проявляется и при больших размерах.

Классификация и терминология

Поверхностное натяжение . Все описанные явления называют «эффектами поверхностного натяжения» и говорят, что жидкость имеет поверхностное натяжение, подобное натяжению растянутой резиновой оболочки. Пока это просто удобное название, которое само по себе не может ничего доказать или объяснить. В лучшем случае оно стимулирует обсуждение и позволяет легко определить, о чем идет речь. В худшем случае — приводит людей к неправильной мысли о том, что на поверхности существует реальная пленка, которую можно содрать с капли, как шнурку с кролика.

Краевой угол . По своей форме лужицы жидкости на столе делятся на два типа.

1) Когда жидкость прилипает к столу и растекается, как на фиг. 112, а , говорят, что жидкость смачивает поверхность стола.

2) Когда жидкость собирается в округлую каплю вопреки действию силы тяжести, как показано на фиг. 112, б , говорят, что она не смачивает поверхности. Если стол наклонить, то такие капли будут скатываться.

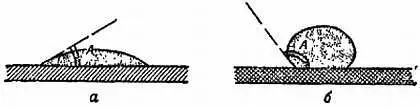
Фиг. 112. Краевой угол.

а— малый угол; б— большой угол.

Эти два случая различаются по углу А (угол внутри жидкости между поверхностью стола и поверхностью жидкости в месте их соприкосновения), который называют краевым углом . Тот же угол существует и на других границах раздела, например в том месте, где поверхность воды встречается со стенками стакана. Если угол А мал, жидкость смачивает твердую поверхность. Это снова только название. Выбрав этот угол и дав ему название, мы ничего не узнали и не объяснили, а лишь облегчили обсуждение [68] Вообще говоря, порой наименования бывают глупые, но некоторые удачны. Скажем, глупо искать особое название для длины стола, на которой находятся лужицы, мало толку было бы и от особого названия для ширины капли. Но оказывается, что угол А заслуживает своего наименования. Величина этого угла является свойством веществ; если вы посмотрите на семейство лужиц, подобных представленным на фиг. 110, в , то увидите, что у всех капель один и тот же угол А . .

Попытка построить теорию

Молекулы. Примем данное химиками определение молекул как мельчайших частиц вещества, из которых построены более крупные предметы, и приведем несколько рассуждений. Хотя такие предметы, как молекулы, видимо, существуют, их в обычный микроскоп не видно (впоследствии, правда, будут приведены убедительные косвенные доказательства их существования), поэтому они должны быть очень малы и многочисленны. Судя по тому, как жидкости льются, их молекулы, очевидно, легко скользят относительно друг друга. Жидкость трудно сжимается; это наводит на мысль, что молекулы в ней расположены тесно. Другие данные, с которыми вы познакомитесь позднее, позволяют думать, что молекулы жидкости постоянно находятся в быстром движении, сталкиваясь друг с другом, подобно людям в толпе, причем с повышением температуры движение это усиливается. Действительно, поведение жидкости можно имитировать с помощью стальных шариков или зерен песка, если эти большие «молекулы» заставить непрерывно вибрировать.

Молекулярные силы: притяжение и отталкивание . Рассмотрим жидкость с точки зрения такой молекулярной картины. Сразу же возникает мысль, что молекулы жидкости сопротивляются их растаскиванию в разные стороны, т, е. притягиваются друг к другу. Вода в наполовину полном кувшине не расширяется и не улетучивается в отличие от газа, который стремится заполнить весь сосуд и быстро улетучивается, или диффундирует. Если сосуд открыт, жидкость остается в сосуде и ее молекулы, по-видимому, притягивают друг друга. Пока мысль о притяжении является лишь смутной догадкой. Именно в поверхностном натяжении, как и в некоторых других явлениях, эта мысль находит основательное подтверждение. Тот факт, что жидкости сильно сопротивляются сжатию, говорит о сопротивлении молекул жидкости более тесному сближению; следовательно, они должны отталкивать друг друга. Таким же образом должны вести себя и молекулы газа при очень тесном сближении [69] При столкновении друг с другом или со стенками сосуда. Что же еще, как не отталкивание от стенок, заставляет газ давить на стенки? , и молекулы твердых тел [70] Можно провести следующую аналогию: молекулы газа соответствуют быстро двигающимся по полю футболистам, которые время от времени сталкиваются между собой; молекулы жидкости подобны людям в толпе вокруг поля: они проталкиваются к центру, чтобы увидеть игру, но остаются в пределах определенных «семейных» групп; молекулы твердых тел подобны таким же болельщикам, рассаженным на трибунах: они азартно вертятся на своих местах. . Например, молекулы указательного и большого пальца отталкиваются при сжатии — какая другая причина могла бы помешать пальцам проникнуть один в другой? Но твердые вещества тоже сопротивляются попыткам растащить их в разные стороны; молекулы этих веществ должны притягивать друг друга. Мы представляем себе, что между молекулами твердых тел действуют два типа сил: силы отталкивания, которые, как показывает опыт, действуют только на очень малых расстояниях, т. е. короткодействующие силы , и силы притяжения, которые действуют на более далеких расстояниях, т. е. дальнодействующие силы . В обычном ненапряженном твердом теле каждая молекула занимает нейтральное положение, так что равнодействующая этих сил равна нулю. При сжатии твердого тела возрастающее отталкивание между молекулами оказывает сопротивление.