Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Опыт 12.Нагрейте кусок стеклянной трубки, растяните его в очень тонкую трубку и опустите один ее конец в чернила (фиг. 122, а ). Окрашенная вода поднимается вверх вопреки силе тяжести, опровергая правило: «вода в сообщающихся сосудах устанавливается на одном уровне». Однако в U-образной трубке с колонами разного сечения жидкость все же устанавливается на одном уровне (фиг. 122, б ). Если вспомнить обсуждение относительной роли поверхностных и объемных эффектов, можно догадаться, что влияние поверхностного натяжения будет более заметно в приборах малых размеров; например, в небольшой U-образной трубке (фиг. 122, в ). Конечно, это то же самое, что мы уже видели при погружении тонкой трубки в чернила.

Наброски, представленные на фиг. 122, г , помогают понять переход от одного опыта к другому. Если жидкость поднимается в тонких трубках, то в еще более тонких она должна подняться еще выше. Проверьте это (см. фиг. 122, д ).

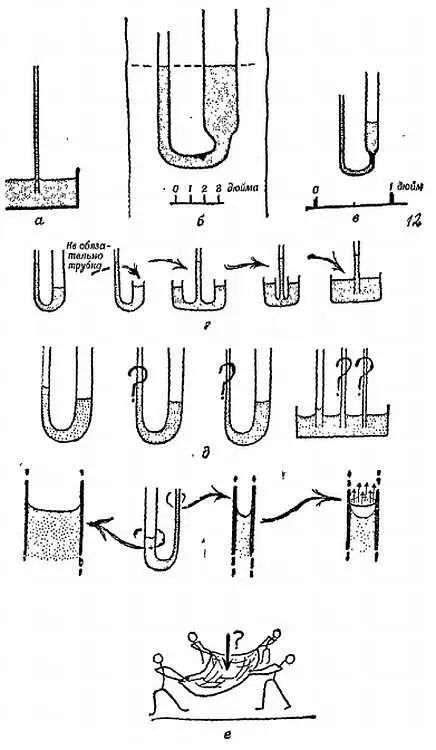
Фиг. 122. Капиллярные явления.

Поскольку это следствие поверхностного натяжения проявляется в трубках, «тонких, как волос», оно получило название от латинского слова «волос» — capilla . Таким образом, капиллярность — это старое название поверхностного натяжения, которое еще применяется, чтобы охарактеризовать поведение жидкостей в тонких трубках. Это красивое название, но оно не объясняет подъема жидкости. Сказать, что вода поднимается по тонкой трубке вследствие капиллярности, по существу то же, что сказать «вследствие поведения тонких трубок». Рассматривая через увеличительное стекло мениск (поверхность жидкости) в тонкой трубке, мы увидим, что он висит, как прикрепленный к стеклу изогнутый мешок, весьма похожий на одеяло пожарников, которые ловят выбрасывающегося из окна горящего дома тяжелого мужчину (фиг. 122, е ).

Снова возникает мысль о резиновой оболочке. Если измерить силы, удерживающие оболочку, то видно, что эти же силы определяют форму маленьких капель. Можно даже говорить, что оболочка удерживает поднимающуюся по трубке жидкость [75] Эта идея может позволить вывести формулу для измерения поверхностного натяжения Т , действующего на каждый сантиметр границы поверхности жидкости: ( тянущая сила со стороны оболочки ) = ( вес жидкости, удерживаемой в трубке ); Т ∙(Длина границы 2π r ) = [Объем (π r 2 )∙(Высота подъема)]∙(Плотность жидкости)∙(Ускорение силы тяжести g ) (эту формулу раньше очень любили составителя экзаменационных вопросов). Таким образом, Т = 1 / 2 g ∙(Плотность)∙(Высота подъема)∙(Радиус трубки). Эта формула более или менее верна, и ее используют для грубых определений Т , но сам вывод граничит с надувательством. На самом деле нет никакой резиновой оболочки, прикрепленной к стеклу, и в реальной формуле Т относится к поверхности раздела жидкость/воздух, а не является силой сцепления со стеклом. Но искривленная поверхность (мениск) реально существует, и, как в любом воздушном шаре, давление «внутри» (над мениском) больше, чем снаружи. С помощью этой разности давлений можно объяснить подъем жидкости в капилляре и дать строгий вывод формулы. , но более реально говорить о молекулах, которые вскарабкиваются по внутренней поверхности трубки и образуют изогнутый мениск.

Жидкости поднимаются не только в круглом стеклянном капилляре. Капиллярность проявляется в любом узком пространстве.

Когда вода стекает между щетинками малярной кисти или увлажняет в ванне ваши волосы, то она заполняет не полые волоски, а узкие промежутки между отдельными волосками. На таком поведении жидкостей основано всасывание масла в ламповый фитиль, воды в банное полотенце и т. д.

Задача 3 (трудная). Формула капиллярности

Допустим, что подъем жидкости в капилляре определяется разностью давлений по обе стороны мениска. Вернитесь к опыту с двумя соединенными друг с другом мыльными пузырями (см. фиг. 111, д ). Какой вывод только из этого опыта можно сделать о соотношении между высотой подъема в капилляре и его диаметром?

Задача 4. Капиллярность в несмачиваемой трубке

Возьмем жидкость, которая образует со стенками трубки большой краевой угол. На фиг. 123 показана, например, ртуть в стеклянной трубке.

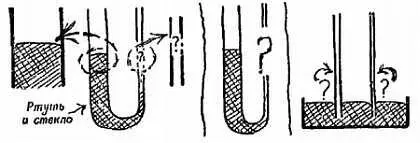
Фиг. 123. К задаче 4.

Уровень ртути в широкой трубке показан, но рисунки не закончены. Набросайте в тетради все эти рисунки и закончите их.

Применения капиллярности

Чтобы жидкость втягивалась в капилляр, а не только поднималась вверх, и вообще проникала в поры, необходим малый краевой угол между жидкостью и стенками пор. При большой величине краевого угла предметы будут оставаться сухими. Ниже приведены примеры, которые демонстрируют роль капиллярности и смачивания в природе и в быту.

1) Системы, где нужен малый краевой угол (желательно при большом поверхностном натяжении)

Вода на волокнах банных полотенец и т. д.

Чернила на конце пера (щель на конце пера подает чернила на бумагу вследствие капиллярности; стальные перья, применявшиеся прежде, когда они бывали новыми, имели большой краевой угол, и для улучшения работы перья следовало смочить слюной).

Чернила на бумаге (но поры в бумаге должны быть закрыты).

Кровь на бинтах.

Капли от насморка на слизистой оболочке носа.

Припой на металле (для уменьшения краевого угла применяют флюс).

? Слюна на пище.

Растворитель для краски на сухом порошке красителя.

Жидкая краска на окрашиваемых поверхностях (с этим связан ряд вопросов в технике живописи).

Мыльная вода при стирке грязной одежды.

? Вода на стеклах очков (здесь нет узких промежутков, но при небольшом краевом угле конденсирующаяся на стекле вода создает плоскую пленку, а не туман из капелек).

2) Системы, где нужен большой краевой угол

Вода на спине утки, на тканях для палаток и зонтов.

? Блинное тесто на сковороде.

Вода на полу в ванной.

? Вода на стеклах очков (мелкие капли быстрее испаряются).

Важную роль капиллярность играет в садоводстве. Вода проникает в тонкие промежутки между частицами почвы. Разрыхление и вскапывание изменяет размеры этих промежутков и затрудняет доступ воды из глубины почвы к поверхности, предотвращая тем самым ее испарение.

Кирпичи пористы. Кирпичные дома на высоте 30 см или более от поверхности земли должны иметь изоляцию от влаги из непористого материала.

Объяснение капиллярности с молекулярной точки зрения