Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Это простое правило проверки баланса — суммарное Mv после столкновения равно суммарному Mv до столкновения — делает количество движения чрезвычайно важной и удобной для расчетов величиной. Изучение механики движущихся тел, будь то планеты или атомы, похоже на выслеживание банды преступников, которые постоянно меняют свой внешний облик. Сыщик выискивает признаки, которые можно, пользуясь услугами тайных агентов, распознать и проследить при любых изменениях внешнего облика (специфическая форма уха, золотой зуб, хромота и т. д.).

Ученые установили, что в механике такой неизменной характеристикой является масса: масса сохраняется, говорят они. В течение столетий считали, что вещество неразрушимо и что химические превращения представляют собой лишь обмен частицами вещества.

Тщательное взвешивание химических веществ в колбе до и после химических реакций не обнаружило измеримых изменений общей массы; поэтому ученые выдвинули утверждение о сохранении массы (которое, как они считали, означает сохранение вещества) в качестве универсального правила. Однако этого правила оказалось недостаточно для полного количественного описания столкновений (а в последнее время мы убедились в том, что правило это в его простейшей форме само по себе неверно). В качестве меры движения тела появилось количество движения Mv , когда было установлено, что эта величиа сохраняется. Цепляясь за величину Mv , как за самый надежный ключ к пониманию движения и его измерению, мы по-прежнему рассматриваем сохранение количества движения как прочную основу механики.

Теперь мы располагаем двумя правилами для любой замкнутой [131]системы:

ПРИ ЛЮБОМ ВЗАИМОДЕЙСТВИИ СУММАРНАЯ МАССА МОСТАЕТСЯ НЕИЗМЕННОЙ

(масса М — скаляр ). Это правило называется законом сохранения массы .

ПРИ ЛЮБОМ ВЗАИМОДЕЙСТВИИ СУММАРНОЕ КОЛИЧЕСТВО ДВИЖЕНИЯ MvОСТАЕТСЯ НЕИЗМЕННЫМ

(количество движения — вектор ). Это правило называется законом сохранения количества движения .

Эти правила позволяют нам делать предсказания или извлечь полезные сведения из измерений. Они представляют собой в известном смысле сущность физики и дают возможность привести природу в стройную систему. (Они напоминают правила проверки бухгалтерского баланса, например: итоговая сумма в графе «приход» должна быть равна итоговой сумме в графе «расход».)

Существуют ли другие подобные правила? Сохраняются ли также величины Mv 2, Mv 3и т. д.? Измерения М и v при столкновениях показывают, что величины Mv 3и Mv 4безусловно не сохраняются, поэтому к ним не проявляют интереса и не присваивают им названий. Что же касается величины Mv 2, то она представляет интерес: в некоторых случаях она сохраняется, а в других случаях переходит в иные формы весьма важной и удобной характеристики, которую мы называем энергией . Величине Mv 2, или, вернее, величине 1/ 2 Mv 2! присвоено наименование кинетическая энергия . Мы вернемся к ней в одной из последующих глав.

Изменение количества движения дается произведением ( сила )∙( время ). Мы увидим, что изменение кинетической энергии дается произведением ( сила )∙( расстояние ). Это простое произведение, содержащее силу и размер, и нет ничего удивительного, что величиной 1/ 2 Mv 2удобно пользоваться.

ПРИМЕРЫ ИЗМЕНЕНИЙ КОЛИЧЕСТВА ДВИЖЕНИЯ

Опыт 2.Грубый опыт со столами на колесах. Студенты А и В сидят на двух столах, снабженных колесиками на шарикоподшипниках (роликовых коньках). Оба стола в начальный момент неподвижны и достаточно удалены друг от друга. Студенты тянут за веревку, и столы сближаются (фиг. 198), пока не столкнутся.

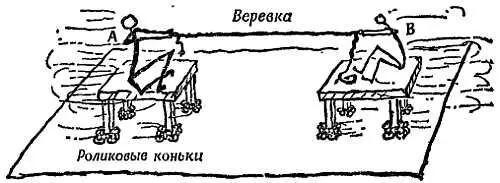
Фиг. 198. Грубый эксперимент.

Если массы (студент + стол) не равны, то туго натянутая веревка сообщает им неодинаковые ускорения. Сближаясь, обе массы приобретают неодинаковые скорости. При столкновении они сводят к нулю количество движения друг друга, и движение прекращается.

Опыт иллюстрирует изменение количества движения, но не дает доказательства его сохранения, если только не измерять приобретаемые количества движения.

Задача 3.

При сближении столов в описанном выше демонстрационном опыте веревка все время туго натянута, ее тянут к себе оба студента или один из них. Предположим, что:

а) студент А крепко держит свой конец веревки, а студент В тянет веревку к себе, поддерживая натяжение постоянным и равным 100 ньютон, или

б) студент В крепко держит свой конец веревки, а студент А тянет веревку к себе, поддерживая натяжение постоянным и равным 100 ньютон, или

в) студенты А и В тянут веревку каждый к себе, поддерживая натяжение постоянным и равным 100 ньютон.

Какие различия вы рассчитываете заметить для этих трех случаев:

1) В относительном движении обоих столов?

2) В движении студента А и стола, на котором он сидит?

( Указание. Студент А и стол обладают определенной массой, к которой приложена сила 100 ньютон.)

3) В количестве веревки, накапливающемся на каждом столе?

Опыт 3. Тележки, расталкиваемые пружиной (фиг. 199).

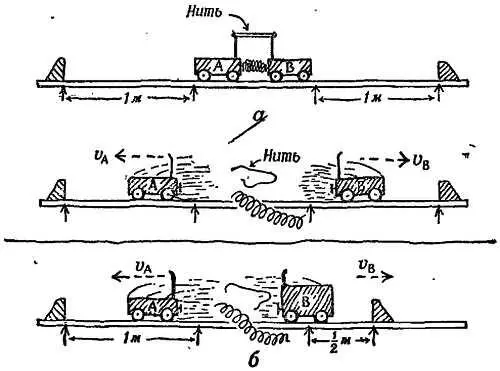
Фиг. 199. Движение тележек, расталкиваемых пружиной.

Две игрушечные тележки помещены посередине рельсового пути, у которого компенсировано трение для движения тележек в разные стороны. Между тележками помещена сжатая пружина, которая стремится оттолкнуть их друг от друга, но тележки связаны нитью. Когда нить пережигают, пружина расталкивает тележки, сообщая каждой из них некоторое количество движения; затем пружина перестает действовать, и тележки движутся равномерно.

Если тележки обладают одинаковыми массами, то, как показывают эксперименты, они движутся с равными и противоположно направленными скоростями, например: если тележка А проходит 1 м до какой-то отметки, то тележка В проходит за это же время 1 м в противоположном направлении. Значит, поскольку скорости равны и противоположно направлены ( v и —v ), а массы равны, количество движения Mv , приобретаемое тележкой В , равно и противоположно по направлению количеству движения —Mv , приобретаемому тележкой А .

Если масса тележки В вдвое больше массы тележки А , то тележка В приобретает вдвое меньшую скорость; если тележка А проходит 1 м, то тележка В проходит за это же время 1/2 м. Если в этом случае тележка А приобретает количество движения —Mv , то тележка В приобретает количество движения 2 M ( 1/ 2 v ), направленное в противоположную сторону.