Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Вывод с использованием математического анализа

F= M∙ a= M∙Δ v/Δ t

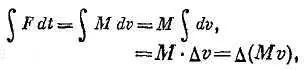
Поскольку М постоянна.

Если F постоянна, то левая часть записывается в виде 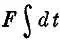, т. е. F ∙Δ t .

Значит,

F∙Δ t= Δ( Mv)

Если F непостоянна, то , «импульс силы», дает произведение ( среднее значение силы )∙Δ t . Тогда можно записать:

(Среднее значение F)∙Δ t= Δ( Mv).

Если М непостоянна (например, масса ракеты, выбрасывающей в полете продукты сгорания), соотношение F= M∙ aнепригодно, но изменение количества движения Δ( Mv) по-прежнему равно или произведению

(Среднее значение F)∙Δ t

Это возвращает нас к определению силы

F= d( Mv)/d t

т. е. сила равна скорости изменения количества движения. Такова первоначальная формулировка Ньютона, которая справедлива даже в теории относительности.

Проработайте предлагаемую ниже задачу на соотношение

F∙Δ t= Δ( Mv)

Соотношение F∙Δ t= Δ( Mv) представляет собой фактически иную форму записи соотношения F= M∙ a и во многих случаях быстрее приводит к цели. Силы следует выражать в ньютонах. Если воспользоваться этим соотношением для вычисления силы, то ответ автоматически получится в ньютонах.

Задача 1(а)

Человек в течение 1/50 сек прикладывает силу 200 ньютон к летящему футбольному мячу, в котором содержится в общей сложности 0,500 кг материала. Насколько быстрее будет двигаться мяч после такого удара?

Приложенная сила равна ___ ньютон.

Время Δt , в течение которого действует сила, равно ___ сек.

Следовательно, увеличение количества движения должно быть равно ___, ньютон∙сек.

( Примечание . Ньютон∙сек должно быть то же самое, что килограмм∙метр/сек.)

Следовательно, поскольку М = 0,500 кг, увеличение скорости должно быть равно ___ м/сек.

Задача 1(б)

Футболист ударяет по покоящемуся мячу массой 0,5 кг и сообщает ему скорость 14 м/сек. Соприкосновение между ногой и мячом длится 1/ 50ceк. Вычислите силу, действовавшую при этом столкновении.

[Вместо более утомительного способа, которым вы решали задачу 9 в гл. 7 , воспользуйтесь здесь соотношением F∙Δ t= Δ( Mv).]

Изменение количества движения равно ___ кг∙м/сек (или ньютон∙сек). Следовательно, действующая сила должна быть равна ___ ньютон.

Эта же сила в «плохих» единицах равна приблизительно ___ кГ.

Задача 1(в)

Футболист ударяет по мячу массой 1/ 2 кг, летящему на него со скоростью 10 м/сек. Мяч отскакивает назад со скоростью 14 м/сек. Столкновение длится 1/ 50сек. Вычислите среднюю действующую силу. (Скорость и количество движения — векторы. Обратите внимание на употребление знаков плюс и минус.)

v 0= —10 м/сек, v = + 14 м/сек, t = 1/ 50 сек.

За 1/ 50 сек. количество движения меняется от ___ до ___ кг∙м/сек.

Изменение количества движения равно ___ кг∙м/сек.

Следовательно, действующая сила равна = ___. ___ (единицы)~= ___ кГ.

Количество движения

Мы называем произведение Mv «количеством движения» (это очень удобная величина, и ею широко пользуются в физике).

Тогда соотношение F∙ t= Δ( Mv) гласит: « Сила , умноженная на время ее действия , равна изменению количества движения » [123].

При внезапном изменении количества движения время зачастую мало и его записывают в виде Δ t , имея в виду «изменение времени дня», например короткий интервал времени между 3 час. 42 мин. 4,60 сек. и 3 час. 42 мин. 4,72 сек. Значит, мы можем писать

F∙Δ t= Δ (количество движения), или Δ( Mv).

Единицы

Поскольку соотношение F∙ t= Δ( Mv) получено из соотношения F= M∙ a, то силу F нужно выражать в тех же абсолютных единицах — ньютонах. Если М дано в кг, a v — в м/сек, то количество движения Mv будет выражено в килограммах, умноженных на м/сек . Это записывают в таком виде [124]: кг∙м/сек. Если Mv выражено в кг∙м/сек, а t — в сек, то F должна быть в ньютонах [125].

Прыжки и столкновения

Попытаемся применить соотношение F∙Δ t= Δ( Mv) в задачах о прыжках, совершаемых людьми, и о столкновениях автомобилей. Мы воспользуемся этим соотношением при решении приводимых ниже задач, а также при построении молекулярной теории газов, где оно позволит нам сделать важные предсказания.

В соотношении F∙Δ t= Δ( Mv) величина F представляет собой реальную силу, именно ту силу, которая необходима, чтобы произвести заданное изменение количества движения за указанный промежуток времени Δ t . Если пол, стена или что-то еще не развивают силы, то количество движения движущегося тела не изменится.

За короткое время может произойти большое изменение Mv , например, когда прыгун опускается на землю или когда автомобиль врезается в стену. В этом случае Δ( Mv ) велико, a Δ t мало

F∙(малое Δ t) = большое Δ( Mv).

Таким образом, сила F должна быть очень велика . При столкновениях развиваются огромные силы, и, хотя они действуют в течение лишь очень коротких промежутков времени, эти силы способны причинить большой ущерб. Чтобы уменьшить F и предотвратить плачевные последствия, нужно увеличивать Δ t . Для этого следует при прыжке сгибать ноги в коленях и надевать мягкую обувь, этой же цели служат эластичные предохранительные маты.

Вратари надевают особые перчатки и, задерживая мяч, следят за тем, чтобы их рука отходила назад для удлинения промежутка времени Δ t , в течение которого мяч останавливается. В гл. 7 , где была приведена задача о прыжке человека на пол, скорость человека изменялась от 5 м/сек до нуля примерно за 1/ 100сек.

В этом случае соотношение F∙Δ t= Δ( Mv) дает

F∙( 1/ 100сек) = (100 кг х 0) — (100 кг х 5 м/сек) =

= —500 кг∙м/сек (или ньютон∙сек),

= —50 000 ньютон

( F выражается в ньютонах, поскольку массу мы выражаем в кг, v — в м/сек; F должна быть выражена в абсолютных единицах)

~= 5000 кГ, или 5 тонн силы.

Это настолько большая сила, что действие ее со стороны пола на ступни, которое передается на позвоночник, недопустимо даже в течение 1/ 100 сек. Не пытайтесь прыгать с таким резким приземлением — можете поплатиться серьезными телесными повреждениями. Но прыжок с высоты 1,2 м можно сделать вполне безопасным. Для этого достаточно просто согнуть ноги в коленях, увеличив Δ t в 10–20 раз по сравнению с 1/ 100сек и тем самым уменьшив в 10–20 раз силу F .