Эрик Роджерс - Физика для любознательных. Том 3. Электричество и магнетизм. Атомы и ядра

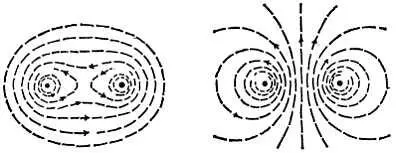
Фиг. 20. Суммарное магнитное поле параллельных токов.

Притяжение между токами, текущими в одном направлении, и отталкивание в случае токов, текущих в противоположных направлениях.

Чтобы вывести нужный закон, начнем с рассмотрения двух длинных параллельных проводников, по которым текут токи I 1a и I 2 a и которые находятся друг от друга на расстоянии d м. Они будут вызывать катапультирующие силы, действующие в поперечном направлении, как показано на фиг. 22. После этого выберем два очень коротких отрезка проводников, находящихся друг против друга, L 1и L 2, и не будем обращать внимания на остальные части проводов. Рассматривая их как части длинных параллельных проводников, можно ожидать, что каждый из отрезков будет окружен круговым магнитным полем. Если токи текут в одном направлении, то катапультирующие силы будут притягивать эти два «элемента тока» друг к другу. (Отрезок L 1, например, по которому течет ток I 1, пересекается магнитными силовыми линиями тока I 2 в проводнике под прямым углом; поэтому на него действует сила — F , направленная слева направо.)

Из опыта, описанного выше, мы знаем, что эта сила изменяется прямо пропорционально току в проводнике:

F~ I 1(из опыта).

Если бы мы увеличили длину отрезка проводника вдвое, соединив последовательно два проводника L 1, то, очевидно, сила, действующая на них, была бы равна двум F , т. е. на удвоенную длину пришлась бы удвоенная сила, т. е. сила, действующая на исследуемый проводник, пропорциональна его ДЛИНЕ.

Фиг. 21. «Элементы токов».

На двух длинных проводниках выбраны короткие участки L 1 и L 2, один напротив другого.

Фиг. 22. Силы, действующие между элементами токов.

Их направление подсказывается видом силовых линий суммарного магнитного поля.

F~ L 1(предположение, оправдываемое мысленным экспериментом или здравым смыслом),

F ~ I 1и F~ L 1или F~ I 1 L 1

Но схема симметрична — кто может сказать, какой из проводников «действует» на другой, создавая магнитное поле, а какой «подвергается действию»?

F~ I 2 L 2 так же, как F~ I 1 L 1

или

F~ ( I 1 L 1)∙( I 2 L 2)

Полный закон взаимодействия должен содержать расстояние между отрезками проводника. Простые опыты показывают, что F уменьшается с увеличением d . Зная это, что вы можете предположить? Наиболее правдоподобное предположение об обратной квадратичной зависимости, будучи подвергнутым опытной проверке, подтверждается. Тогда

F~ ( I 1 L 1)∙( I 2 L 2)/ d 2

или

F = B∙[( I 1 L 1)∙( I 2 L 2)/ d 2]

где В — общий постоянный множитель.

Однако от закона в такой форме пользы мало. Необходим множитель, который бы учитывал отклонения направлений от параллельных и перпендикулярных — этих отклонений мы будем стараться избегать, выбирая простейшие геометрические условия. В опытах мы пользуемся замкнутыми цепями, так что будем считать L 1, короткой стороной длинного прямоугольного витка (а впоследствии участком траектории электрона). Для удобства мы возьмем не один короткий отрезок L 2, а много таких отрезков, соединенных последовательно, и образуем из них кольцевой виток, в центре которого будет располагаться L 1(фиг. 23, 24). Тогда вокруг каждого из отрезков, образующих виток и несущих ток I 2а, возникнет кольцевое магнитное поле, пересекающее отрезок L 1, расположенный в центре, и каждый из кусочков кольца будет расположен на расстоянии R , равном радиусу кольца, от L 1. Тогда сила, действующая на L 1, дается выражением

F = B∙[( I 1 L 1)∙( I 2∙первый отрезок L 2)/ R 2] + B∙[( I 1 L 1)∙( I 2∙второй отрезок L 2)/ R 2] + и т. д. (по всем отрезкам L 2, образующим кольцо) =

F = B∙[( I 1 L 1)∙( I 2)/ R 2] (первый отрезок L 2+ второй отрезок L 2+ по всему кольцу) =

F = B∙[( I 1 L 1)∙( I 2∙2π R)/ R 2]

Если кольцо содержит N витков, то

F = B∙[( I 1 L 1)∙( I 2∙2π R∙N)/ R 2]

Сформулировав предполагаемый закон, мы проверяем его, измеряя силу, действующую на короткую сторону прямоугольной рамки с током, помещенной в центр кольцевого витка, по которому также течет ток. Пример такого рода изображен на фиг. 23, 24. Без экспериментальной проверки придется поверить этому закону на слово.

Фиг. 23. Проверка закона катапультирующих сил с помощью элементов токов.

Измеряется сила, действующая на короткую сторону L 1. Кольцевой виток, несущий ток I 2, рассматриваем как последовательность коротких отрезков, отстоящих от центра на расстояние R .

Фиг. 24. Определение катапультирующей силы для частичной проверки закона.

а— длинный виток подвешен на коромысле весов, и ток на него подается через чашечки со ртутью; б— длинный виток кладется на рычажные весы, и ток также подводится через чашечки со ртутью.

Определение постоянной В

Если в демонстрационном опыте, подобном тому, который изображен на фиг. 24, мы выполним все необходимые измерения (т. е. определим все линейные размеры, измерим оба тока и силу), то после этого сможем оценить постоянную В . Точные измерения дают значение В = 0,000000100,т. е. 10 -7. Это и в самом деле круглое число 1/10 000 000, поскольку величина ампера выбрана так, чтобы сделать его круглым. Следовательно, в нашем определении ампера через скорость осаждения меди мы вынуждены использовать некруглое число 0,000 000 329 кг меди в 1 сек. Отныне мы будем писать 10 -7вместо В , чтобы избежать путаницы — ведь есть другая постоянная , которую мы использовали при записи закона Кулона, определяющего силу, действующую между зарядами. Используя «закон катапульты», нужно помнить, что 10 -7 — не просто число вроде 2 π , а имеет размерность:

B= 10 -7 ньютон∙м 2/а 2∙м 2 = 10 -7 ньютон/а 2

Поразительное предсказание Максвелла

(Рассуждения, приведенные ниже, слишком трудны для элементарного объяснения; скорее всего этот параграф останется загадкой. Можете его пропустить, если хотите, а можете и прочитать, чтобы познакомиться с рядом удивительных выводов.)