Фрэнк Вильчек - Красота физики. Постигая устройство природы

• Из сути строения материи – музыка . Не было никакой логической причины ожидать, что математика, разработанная для понимания музыки, должна иметь что-то общее с атомной физикой. Тем не менее оказалось, что одни и те же понятия и уравнения управляют обоими царствами. Атомы – это музыкальные инструменты, и свет, который они испускают, делает их звучание видимым.

• Из прекрасных законов – прекрасные объекты. Основные законы не постулируют существование атомов. Атомы появляются как следствие из них и при этом – как прекрасные объекты (см. вклейку СС). Описанные математически физические атомы – это трехмерные объекты, которые под влиянием одухотворенного таланта художника порождают образы исключительной красоты.

• Из динамики – постоянство. Основные законы – это уравнения, описывающие, как окружающий нас мир меняется во времени. Но у этих уравнений есть некоторые важные решения, которые не меняются во времени. Эти решения, и только они, описывают атомы, из которых состоит наш повседневный мир и мы сами.

• От непрерывности – к дискретности . Волновые функции, которые описывают электроны в атомах, – это поля вероятности (распределения вероятностей), которые наполняют пространство. Они непрерывны и напоминают облака. Но устойчивые формы облаков различимы по отдельности и несут на себе отметины Чисел.

Во время зарождения современной квантовой теории, конечно, никакого учебника по ней еще не было. Так называемые практики, жаждущие воспользоваться новой атомной теорией, вместо учебника обратились к другому предмету – книге лорда Рэлея «Теория звука». Именно там они нашли математику, необходимую для описания того, как работают атомы. Она была разработана ранее – для описания работы музыкальных инструментов! Хотя символы здесь обозначают другие вещи, в сущности появляются те же самые уравнения, для решения которых используются те же самые приемы. Пифагор был бы доволен.

Физика музыкальных инструментов есть физика стоячих волн . Стоячие волны – это волны, существующие в конечных объектах или в ограниченном пространстве. Так, колебания струн музыкальных инструментов или звуковых дек и резонаторов в них – это стоячие волны, которые должны быть противопоставлены бегущим волнам . Например, когда мы говорим о звуковых волнах, мы обычно имеем в виду бегущие волны, которые распространяются или разбегаются от источника. Колебания крышки рояля, являющиеся стоячими волнами, толкают окружающий воздух в разные стороны. Движение части воздуха оказывает давление на другие части воздуха вокруг, которые оказывают давление на следующий слой воздуха, и т. д. В результате возникает возмущение, живущее своей собственной жизнью.

Стоячие волны – это вид движения, который вы создаете в налитой в ванну воду, когда шлепаете по ней или который наблюдается в колебаниях гонга или камертона после того, как их задели. В каждом из этих случаев – в шлепке по воде в ванне, ударе по гонгу или камертону – после шумного старта движение будет стабилизироваться, пока не станет регулярным в пространстве и периодическим по времени. В этом состоит суть камертона: он «хочет» вибрировать с определенной частотой и, таким образом, производит верный чистый звук. Обычный гонг производит более сложную и интересную комбинацию звуковых тонов. Мы скоро вернемся к этому вопросу.

Мы можем осветить йогу музыкальных инструментов более ясно, рассмотрев предельно простой инструмент, который на самом деле является пифагоровым, – туго натянутую струну, зажатую с двух концов (илл. 24). В простой одномерной геометрии отрезка конечной длины мы можем с первого взгляда отыскать естественный образец стоячей волны.

На иллюстрации сплошные и пунктирные линии показывают форму струны в различные моменты времени, демонстрируя четыре различных состояния стоячей волны (амплитуда, т. е. размер отклонения струны от средней линии, на иллюстрации сильно преувеличена, чтобы можно было ясно видеть саму волну). В промежуточные моменты точки на струне перемещаются вверх и вниз; составленная из них сплошная линия последовательно переходит в пунктирную, и наоборот, циклически.

Простые требования геометрии привносят целые числа и дискретность в описание этих непрерывных по сути фигур. Последние должны умещаться на длине струны! Идя сверху вниз и сравнивая картины, мы видим, что темпы изменений при движении вдоль струны слева направо отличаются по скорости в два, три, четыре раза.

Можно получить естественные колебания, которые соответствуют трем циклам, или двум, или четырем, или любому целому числу, но ничего между целыми числами быть не может . В результате естественные частоты нашего инструмента дискретны или, как мы говорим, квантованы .

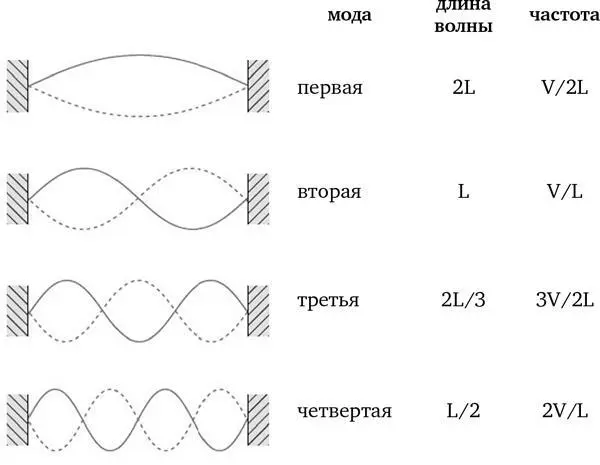
Илл. 24. В простой одномерной геометрии отрезков конечной длины мы можем с первого взгляда отыскать естественные образцы стоячей волны. Они должны умещаться на длине отрезка! Эти простые геометрические правила требуют целых чисел и дискретности в описании поведения непрерывного объекта.

В отличие от ставшей притчей во языцех сферической коровы [55] Рассказывают, что на некой ферме коровы давали мало молока, поэтому фермер обратился в местный университет с просьбой о помощи. Приехала команда профессоров, возглавляемая физиком-теоретиком. Вскоре после этого физик вернулся на ферму и сказал фермеру: «У меня есть решение, но оно работает только для сферических коров в вакууме». – Прим. пер. , наш пифагоров музыкальный инструмент не так оторван от реальности. Куда важнее, что урок, который мы извлекли из этого простого инструмента, – о том, что геометрические ограничения для конечных объектов ведут к дискретности (квантованию) их естественных форм колебаний и, следовательно, их естественных частот, – является идеально всеобъемлющим. Как мы вскоре увидим, в квантовой механике этот урок становится стержнем атомной физики.

Вы также можете получить стоячие волны деки гитары, когда дергаете ее струну, или квадратной пластины, когда ударяете по ней (илл. 25), причем волны можно сделать видимыми. Основная идея остается той же, что и та, которую мы обсуждали в случае с закрепленной струной. Стоячая волна – это движение вверх-вниз, которое в одних местах выше (или, на нашем жаргоне, имеет большую амплитуду), чем в других. Существуют линии, вдоль которых отклонение исчезает и движение отсутствует. Точки этих линий называются узлами, а сами линии – узловыми линиями. Если вы насыплете на пластину немного песка, то он соберется вдоль узловых линий – именно это вы видите на рисунке.