Дэйв Голдберг - Вселенная в зеркале заднего вида. Был ли Бог правшой? Или скрытая симметрия, антивещество и бозон Хиггса

Очевидная изотропия вселенной — то есть то обстоятельство, что она более или менее одинакова по всем направлениям — предполагает, по крайней мере, вероятность наличия еще одной физической симметрии.

Вращательная симметрия:законы физики не меняются, если повернуть систему в целом.

А это заставляет нас вернуться к вопросу, с которого начался наш разговор — ура-ура, мы о нем не забыли: к вопросу о том, почему ночью темно. Повторяю, довода, что Солнце находится по другую сторону от Земли, недостаточно. Разумеется, это правда, но правда и то, что Солнце — не единственная звезда во вселенной. Звезд на небе столько, что, если вдуматься в цифры, непонятно, почему они не поджарят нас в мгновение ока.

Мы уже убедились, что вселенная очень велика, а может быть, и бесконечна. Если она и в самом деле более или менее одинакова по всем направлениям, то чем дальше от Земли заглянешь, тем больше звезд увидишь. С другой стороны, чем они дальше, тем тусклее.

Сфера Дайсона

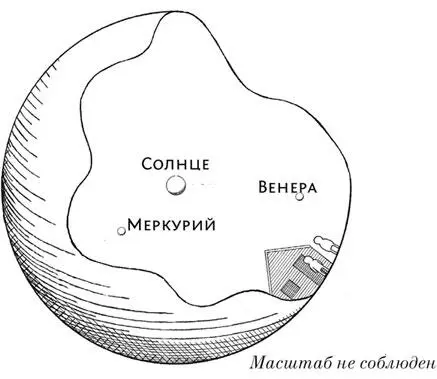
Так что же перевешивает — практически бесконечное множество звезд в небе, каждая, по грубым прикидкам, такой же собственной яркости, что и Солнце, или тот факт, что каждая звезда в отдельности тусклая? Чтобы оценить оба эти эффекта, я снова прибегну к симметрии, а попутно при помощи наглядных иллюстраций покажу, как искать внеземные цивилизации.

В 1960 году Фриман Дайсон, физик и футурист из Принстона, предложил способ искать крайне высокоразвитые цивилизации. Раса, достигшая очень высокого уровня технологического прогресса, могла бы построить вокруг своей звезды гигантскую сферу (в научной фантастике они так и называются — сферы Дайсона), которая улавливала бы все падающее на нее излучение. Излучение исходит от звезды симметрично, это функция как симметричной природы электромагнитного поля, так и того факта, что звезды представляют собой почти идеальные сферы. Сфера Дайсона улавливает излучение равномерно по всей поверхности, и если выстроить ее на соответствующем расстоянии от звезды-родительницы, вся ее внутренняя поверхность станет обитаемой.

Для наглядности представьте себе, что если бы мы выстроили сферу Дайсона радиусом приблизительно в одну астрономическую единицу (тогда температура на ее поверхности будет примерно равна комнатной), количество доступной недвижимости возросло бы в несколько миллиардов раз по сравнению с нынешним. Вот это я понимаю — падение рынка! Зато проблема перенаселенности будет решена — на сфере хватит места квинтильонам. Однако, даже если не вдаваться в технические детали, сразу можно сказать, что главной загвоздкой станет недостаток сырья для строительства подобного сооружения.

Дайсон понимал, что все впитанное излучение в конечном итоге будет излучено дальше. Внешняя сторона сферы будет балансировать примерно на уровне комнатной температуры и в конце концов испустит инфракрасное излучение обратно во вселенную.

На самом деле Дайсон не предлагал нам строить гигантскую сферу вокруг Солнца. Нет, он считал, что подобная идея могла бы прийти в голову сверхцивилизациям — и тогда мы бы могли найти сверхцивилизации путем поиска гигантских источников инфракрасного излучения. Правда, если учесть немыслимое могущество подобных цивилизаций, неясно, так ли уж хорошо было бы для нас наладить с ними контакт. Как-то сразу представляешь себе комара, присевшего на спину тираннозавру.

Представьте себе, что мы построили сферу с радиусом не в одну астрономическую единицу, а в две — то есть она вдвое дальше от Солнца. В нашей Солнечной системе она примерно совпадет с внутренним краем пояса астероидов — перед самым Юпитером. Материалов нам понадобится гораздо больше. Если удваиваешь радиус сферы, площадь поверхности возрастает в четыре раза. Квадратное соотношение, сами понимаете. Однако это означает, что количество излучения, доходящего до любой точки на сфере, сокращается — тоже в четыре раза. Яркость источника обратно пропорциональна квадрату расстояния до него.

Закон обратных квадратов открыл не Дайсон. Он известен со времен античности и появляется в самых разных контекстах. Чем дальше галактика, тем тусклее она становится — пропорционально квадрату расстояния до нее.

Обратному квадрату расстояния пропорциональна и гравитация. Чем дальше находишься от Солнца или от центра Земли, тем слабее сила гравитации. Она также при удвоении расстояния сокращается в четыре раза. Соотношение между силой гравитации и законом обратных квадратов стало катализатором, подтолкнувшим Исаака Ньютона к публикации в 1687 году « Principia Mathematica ». В этом труде он сформулировал основы многого из того, что мы теперь называем физикой, и представил соответствующие формулы, в том числе и свои знаменитые законы движения. Очень может быть, что все это он опубликовал на спор.

В 1684 году Эдмунд Галлей (тот самый, с кометой), Кристофер Рен и Роберт Гук — выдающиеся ученые своего времени — обсуждали, почему планеты вращаются по эллиптическим орбитам. Вспомним, что этот факт открыл Кеплер на основании наблюдений за 75 лет до этого. Рен даже предложил денежное вознаграждение всякому, кто предоставит ему решение этой задачи.

Галлей был убежден, и вполне справедливо, что планеты притягиваются к Солнцу с силой, пропорциональной обратному квадрату расстояния, но дальше продвинуться не смог. Поэтому он обратился к Ньютону. Ньютон тогда еще не опубликовал труд всей своей жизни, однако уже был профессором в Кембридже и пользовался заслуженной славой гения первой величины. Вот как писал об этом случае современник:

В 1684 году доктор Галлей посетил Кембридж и, проведя некоторое время в обществе сэра Исаака, спросил его, какой, по его мнению, должна быть кривая, описываемая планетами, если предположить, что сила притяжения к Солнцу обратно пропорциональна расстоянию до него.

Сэр Исаак тут же ответил, что это должен быть эллипс. Доктор, преисполнившись радости и изумления, спросил, откуда ему это известно.

— Видите ли, я это вычислил, — сказал тот.

Общепринятая точка зрения состоит в том, что Ньютон все это вывел лет за 25 до описываемой беседы, когда вернулся домой из школы, поскольку занятия отменили из-за эпидемии чумы. Так ли это, неясно. Ясно другое: черновики Ньютон не нашел и поэтому пообещал Галлею повторить выкладки. Три года спустя, в 1687 году, он опубликовал « Principia ». В данных обстоятельствах Галлей, похоже, поступил не по-джентльменски, забрав себе денежный приз, который предлагал Рен.