Константин Ефанов - Аппараты с перемешивающими устройствами

Оформление конструкции соосного узла АВО реализуется так же через редуктор, как и на аппаратах с мешалками.

В настоящее время при проектировании технологических установках в специальных программах производится расчет параметров аппарата на технологической схеме. Замет вызывается специальный модуль программы, в который передаются полученные данные и выполняется технологический расчет аппарата. Результатом является эскиз аппарата, который используется для проектирования конструкции.

Методы расчета потоков в аппаратах основаны на критериальных методиках гидравлики.

Расчет вычислительными методами гидродинамики, основанными на численном решении дифференциальных уравнений и учитывая при необходимости кинетики химических реакций, может реализован в специальных компьютерных пакетах расчетов методом конечных элементов.

Сравнивая два похода расчетов по критериальным методикам и методом конечных элементов, можно использовать расчет МКЭ для точного проектирования после технологического расчета по критериальным методикам. При проектировании аппарата по аналогу или с нуля по техническому заданию расчет по методу конечных элементов может применяться сразу.

Сравним теоретическое основание программ двух видов.

Нобелевский лауреат, академик Л.Д. Ландау в работе [5,с.12] отмечает: «… замечания о характере изложения гидродинамики … гидродинамику как часть теоретической физики… чтобы создать по возможности более ясную картину явлений и их взаимоотношений. … мы не излагаем в ней как приближенных методов гидродинамических расчетов, так и тех из эмпирических теорий, которые не имеют более глубокого физического обоснования »».

Критреиальные зависимости введены для возможности решения уравнений гидродинамики с использованием эмпирических результатов и методика не является теоретически точной в отличии от методов вычислительной гидродинамики.

В настоящее время при доступности программных пакетов, расчет процессов перемешивания должен выполняться точными методами гидродинамики.

Васильцов в работе [1,с.81] указывает, что для решения ряда технологических задач явлений переноса для быстроходных мешалок используется уравнение Кафарова [7,с.200]:

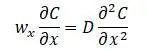
Это уравнение получается из уравнения полной производной концентраций [7,с.198]:

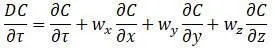
Кафаров отмечает [7,с.200], что последнее уравнение должно быть проинтегрировано совместно с уравнениями движения и сплошности в граничных условиях турбулентного потока, что вызывает непреодолимые трудности. И поэтому производится замена на критериальные уравнения.

В настоящее время с применением компьютерных пакетов МКЭ численных расчетов таких трудностей не возникает и можно получать более точные и обоснованные результаты расчета.

__

Рассмотрим критериальную методику расчета аппаратов с мешалками.

Самой простой моделью является модель реактора идеального смешения периодического или непрерывного. Эта модель не показывает структуру потоков в аппарате, а показывает изменение концентрации вещества в потоке.

Для модели идеального смешения вещество мгновенно равномерно распределяется по всему объему аппарата [6,с.111]. По этой модели можно определить необходимый объем аппарата через время пребывания, которое находится по кинетическому уравнению реакции. В этом аспекте модель полезна, в остальном некорректна.

Время пребывания и объем реактора связаны по формуле [7,с.111]:

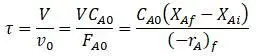
Уравнение в графической форме [6,с.112]:

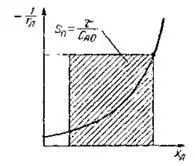
Схема модели [6,с.110]:

Условия в проточном аппарате смешения не совпадают с условиями в периодическом аппарате смешения [7,с.111]. Только при рассмотрении состояния реакционной массы в конкретный момент времени появляется соответствие между аппаратами. Поэтому проточный аппарат является аппаратов дифференциального типа.

Существует более сложная ячеечная модель [6,с.172], в которой перемешиваемый поток разделяется на ряд последовательно соединенных ячеек. В каждой ячейке происходит полное перемешивание потока, при этом перемешивание между ячейками отсутствует. Количество ячеек является характеристикой реального потока. При одной ячейке получается реактор идеального смешения, при бесконечном числе ячеек получается реактор идеального вытеснения.

Ячеечная модель аналогична каскадному соединению аппаратов идеального смешения.

В работе [7,с.238] отмечается, что степень не идеальности потока как фактор не поддающийся расчету. Однако, методами вычислительной гидродинамики структура потока рассчитывается полностью.

Кафаров отмечает [6,с.177] источники неравномерности потока по времени пребывания:

– неравномерность профиля скоростей,

– турбулизация потоков,

– молекулярная диффузия,

– застойные зоны,

– каналообразование, байпасный и перекрестный ток,

– температурные градиенты перемешиваемых потоков,

– теплообмен и массообмен между перемешиваемыми фазами.

Все перечисленные Кафаровым источники неравномерности без затруднений определяются методами вычислительной гидродинамики при расчете в специальных компьютерных пакетах.

В моделях смешения для учета неидеальности потока вводятся функции I-распределения и E-распределения.

Кафаров приводит формы кривых распределения [6,с.179]:

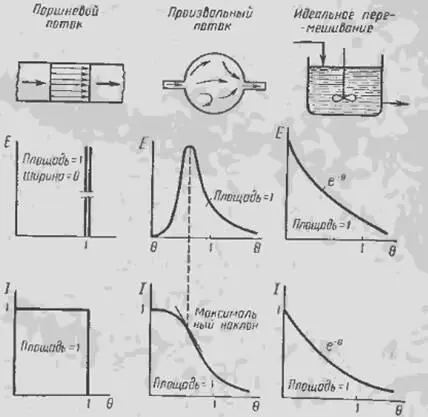
Вводится безразмерное время:

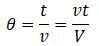
В работе [7,с.241] приводятся кривые I-θ и Е-θ (площади кривых равны единице):

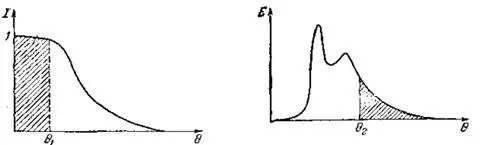
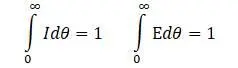
I -функция характеризует время присутствия внутри аппарата, Е-функция характеризует плотность распределения времени пребывания потока в сосуде.

Для выбранного времени θ 1 на кривой I - θ: