А. Березовчук - Физическая химия: конспект лекций

dF = TdS – pdV – SdT,

F – полный дифференциал.

Увеличение объема приводит к тому, что изохорно-изотермический потенциал уменьшается (тот «минус», который стоит перед Р ). Повышение температуры приводит к тому, что F уменьшается.

δ А равн > δ А неравн

Q = Δ U + A,

A = Q – Δ U,

A = T(S 2– S 1) – (U 2– U 1),

А = F 1– F 2= – Δ F,

А равн = – Δ F –

физический смысл изохорно-изотермического потенциала.

Убыль изохорно-изотермического потенциала равна максимальной работе, производимой системой в этом процессе; F – критерий направленности самопроизвольного процесса в изолированной системе. Для самопроизвольного процесса: AF T г< 0.

Для несамопроизвольного процесса: Δ F T,V > 0. Для равновесного процесса: Δ F T,V = 0.

Δ F V,T ≤ 0.

Изохорно-изотермический потенциал в самопроизвольных процессах уменьшается и, когда он достигает своего минимального значения, то наступает состояние равновесия (рис. 4).

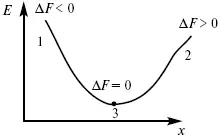
Рис. 4

где 1 – самопроизвольный процесс;

2 – несамопроизвольный процесс;

3 – равновесный процесс.

Изобарно-изотермический потенциал.

1) G (P, Т= cоnst), энергия Гиббса

G = U – TS + PV = H – TS = F + PV,

δ Q = dU – Pdv + A′,

δ A′ = Q – dU – pdv,

δ A′ max = T(S 2– S 1) – (U 2– U 1) – p(V 2– V 1),

δ A′ max = (U 1– TS 1+ PV 1) – (U 2– TS 2+ PV 2) = G 1– G 2= – Δ G,

U – TS + pV = G,

A′ max = – Δ G.

Работа изобарно-изотермического процесса равна убыли изобарно-изотермического потенциала – физический смысл этой функции;

2) функция – полный дифференциал, однозначна, конечна, непрерывна.

G = U – TS + pV,

dG = dU – TdS – SdT + pdv + vdp,

dG = TdS – pdV – TdS – SdT + pdv + vdp,

dG = –SdT + Vdp,

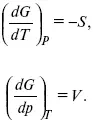
Повышение температуры приводит к тому, что изобарно-изотермический потенциал уменьшается, так как перед S стоит знак «минус». Повышение давления приводит к тому, что изобарно-изотермический потенциал увеличивается, так как перед V стоит знак «плюс»;

3) G как критерий направленности процесса в изолированной системе.

Для самопроизвольного процесса: (Δ G ) P,T < 0. Для несамопроизвольного процесса: (Δ G ) P,T > 0. Для равновесного процесса: ( Δ G) P,T= 0

Δ G (P, T)≤ 0.

Изобарно-изотермический потенциал в самопроизвольных процессах уменьшается, и, когда он достигает своего минимума, то наступает состояние равновесия.

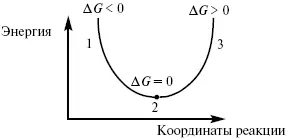
Рис. 5

где 1 – самопроизвольный процесс;

2 – равновесный процесс;

3 – несамопроизвольный процесс.

Совершается работа за счет Δ U и Δ H .

Противодействующие факторы.Энтальпийный фактор характеризует силу притяжения молекул. Энтропийный фактор характеризует стремление к разъединению молекул.

Энтальпия – Н Внутренняя энергия – U.

H = U + PV,

dH = dU + pdv + vdp,

U = TS – PV,

dU = TdS – SdT + pdV + Vdp,

dH = –pdV + pdV + Vdp; U = TdS + VdP.

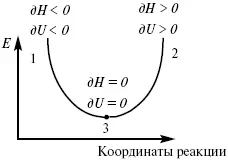
Рис. 6

где 1 – самопроизвольный процесс,

2 – несамопроизвольный процесс,

3 – равновесный процесс,

(dH) P,T≤ 0,

(dU) S,T≤ 0.

Уравнения Гиббса – Гельмгольца – уравнения максимальной работы.

Они позволяют установить связь между максимальной работой равновесного процесса и теплотой неравновесного процесса

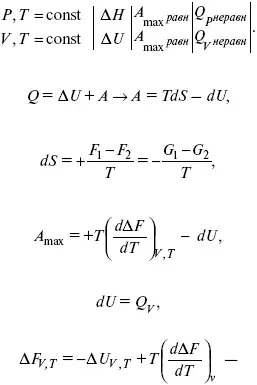
уравнение Гельмгольца (уравнение связывающее функции F и G с их температурными производными).

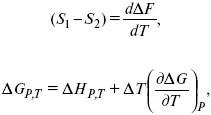
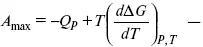
уравнение Гиббса (уравнение связывающее функции F и G с их температурными производными).

Уравнения эти дают возможность рассчитать работу через температурный коэффициент функции Гельмгольца или через температурный коэффициент функции Гиббса.

Уравнение Клаузиуса-Клапейрона

Оно позволяет применить второй закон термодинамики к фазовым переходам. Если рассчитать процессы, в которых совершается только работа расширения, то тогда изменение внутренней энергии

U 2– U 1= T(S 2– S 1) – P(V 2– V 1),

(U 1– TS 1+ PV 1) = (U 2– TS 2+ PV 2),

G 1= G 2– в условиях равновесия.

Предположим, что 1 моль вещества переходит из первой фазы во вторую.

I фаза => dG 1= V 1dp – S 1dT.

II фаза => dG 2= V 2dp – S 2dT, при равновесии dG 2– dG 1= 0

dG 2– dG 1= dp(V 2– V 1) – dT(S 2– S1) –

нет условного равновесия,

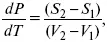
где dP/dT – температурный коэффициент давления,

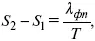
где λ фп– теплота фазового перехода.

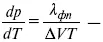
уравнение Клаузиуса-Клапейрона, дифференциальная форма уравнения.

Уравнение устанавливает взаимосвязь между теплотой фазового перехода, давлением, температурой и изменением молярного объема.

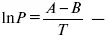
эмпирическая форма уравнения Клаузиуса-Клапейрона.

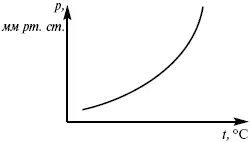
Рис. 7

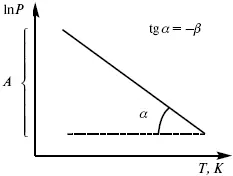
Рис. 8

Уравнение Клаузиуса-Клапейрона изучает фазовые переходы. Фазовые переходы могут быть I рода и II рода.

I рода – характеризуются равенством изобарных потенциалов и скачкообразными изменениями S и V.

II рода – характеризуются равенством изобарных потенциалов, равенством энтропий и равенством молярных объемов.

I рода – Δ G = 0, Δ S ≠ 0, Δ V ≠ 0.

II рода – Δ G = 0, Δ S = 0, Δ V = 0.

Алгебраическая сумма приведенных теплот для любого обратимого кругового процесса равна нулю.