А. Березовчук - Физическая химия: конспект лекций

Эта подынтегральная величина – дифференциал однозначной функции состояния. Эта новая функция была введена Клаузиусом в 1865 г. и названа энтропией – S (от греч. «превращение»).

Любая система в различном состоянии имеет вполне определенное и единственное значение энтропии, точно так же, как определенное и единственное значение Р, V, T и других свойств.

Итак, энтропия выражается уравнением:

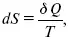
где S – это функция состояний, изменение которой dSв обратимом изотермическом процессе перехода теплоты в количество Q равно приведенной теплоте процесса.

При независимых переменных U (внутренняя энергия) может обозначаться U ВНи V (объем), или Р (давление) и Н (энтальпия). Энтропия является характеристической функцией. Характеристические функции – функции состояния системы, каждая из которых при использовании ее производных дает возможность выразить в явной форме другие термодинамические свойства системы. Напомним, в химической термодинамике их пять:

1) изобарно-изотермический потенциал (энергия Гиббса) при независимых переменных Т, Р и числе молей каждого из компонентов и.;

2) изохорно-изотермический потенциал (энергия Гельмгольца) при независимых переменных Т, V, n i ;

3) внутренняя энергия при независимых переменных: S, V, n i ;

4) энтальпия при независимых переменных: S, Р, п i ;

5) энтропия при независимых переменных Н, Р, n i ..

В изолированных системах (U и V= const) при необратимых процессах энтропия системы возрастает, dS > 0; при обратимых – не изменяется, dS = 0.

Связь энтропии с другими термодинамическими параметрами

Для того, чтобы решить конкретную задачу, связанную с применением энтропии, надо установить зависимость между ней и другими термодинамическими параметрами. Уравнение dS = δ Q/T в сочетании с δ Q = dU + PdV и δ Q = dH – VdP дает уравнения:

dU = TdS – PdV,

dH = TdS + VdP.

Записав уравнение:

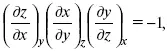
применительно к функциональной зависимости φ(Т, V, S) = 0, получим

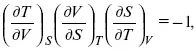
т. е.

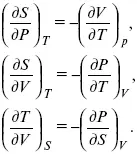
Теперь найдем зависимость энтропии от температуры из уравнений:

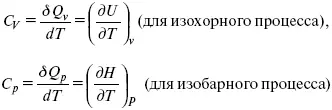
и

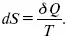
Вот эти зависимости:

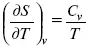
и

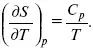
Эти два уравнения являются практически наиболее важными частными случаями общего соотношения:

TdS = CdT.

Пользуясь разными зависимостями, можно вывести другие уравнения, связывающие термодинамические параметры.

Самопроизвольные– процессы, которые идут сами собой, на них не затрачивается работа, они сами могут производить ее (движение камней в горах, натрий с большой скоростью движется по поверхности, так как идет выделение водорода), а калий буквально «прыгает» по воде.

Несамопроизвольные– процессы, которые не могут идти сами собой, на них затрачивается работа.

Равновесие делится на устойчивое, неустойчивое и безразличное.

Постулаты второго закона термодинамики.

1. Постулат Клаузиуса – «Не может быть перехода тепла от менее нагретого к более нагретому телу».

2. Постулат Томсона – «Теплота наиболее холодного тела не может служить источником работы».

Теорема Карно-Клаузиуса:«Все обратимые машины, совершающие цикл Карно с участием одного и того же нагревателя и одного и того же холодильника, имеют одинаковый коэффициент полезного действия, независимо от рода рабочего тела».

Аналитические выражения второго закона термодинамики.

1. Классическое уравнение второго закона термодинамики

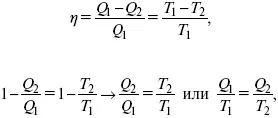
где Q /Т – приведенное тепло;

Q 1/Т 1– приведенное тепло нагревателя;

Q 2/ T 2– приведенное тепло холодильника;

Q 1/Т 1= Q 2/ T 2– равенство приведенных теплот нагревателя и холодильника. Это второе уравнение термодинамики.

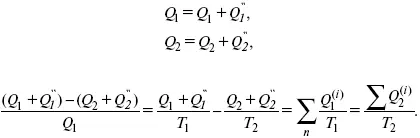
Если делим адиабатами на множество циклов Карно, то получим

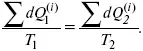
Это третье уравнение второго закона термодинамики для бесконечно малого цикла Карно.

Если процесс является конечным, то

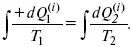
Это четвертое уравнение второго закона термодинамики

Если процесс является замкнутым, то

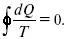
Это пятое уравнение второго закона термодинамики для обратимого процесса.

Интеграл по замкнутому контуру – интеграл Клаузиуса.

При необратимом процессе:

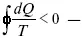
шестое уравнение второго закона термодинамики, или уравнение Клаузиуса, для обратимого процесса равно нулю, для необратимого процесса оно меньше 0, но иногда может быть больше 0.

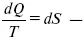
это седьмое уравнение второго закона термодинамики. Второй закон термодинамики – закон роста S.

S = k ln W.

Термодинамическая вероятность

S = k ln W –

это формула Больцмана,

где S – энтропия – степень разупорядоченности системы;

k– постоянная Больцмана;

W – термодинамическая вероятность системы макросостояний.

Термодинамическая вероятность– число микросостояний данной системы, с помощью которых можно реализовать данное макросостояние системы (Р, Т, V).

Если W = 1, то S = 0, при температуре абсолютного нуля –273°С все виды движений прекращаются.

Термодинамическая вероятность– это число способов, которыми атомы и молекулы можно распределить в объеме.

Цикл Карно– круговой тепловой процесс, в результате которого некоторое количество тепла термодинамически обратимым способом переносится от горячего тела к холодному. Процесс должен совершаться таким образом, чтобы тела, между которыми происходит непосредственный обмен энергией, находились при постоянной температуре, т. е. и горячее и холодное тела считаются настолько большими тепловыми резервуарами, что температура первого при отнятии и температура второго при прибавлении рассматриваемого количества тепла ощутимо не изменяются. Для этого необходимо «рабочее тело». Рабочим телом в этом цикле является 1 моль идеального газа. Все процессы, составляющие цикл Карно, являются обратимыми. Рассмотрим их. На рисунке 9 показано: