Роджер Пенроуз - Новый ум короля: О компьютерах, мышлении и законах физики

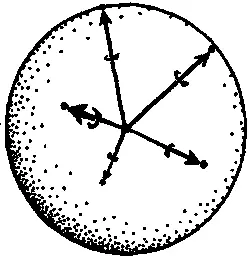
Рис. 6.29.Общее состояние с высшим спином для массивной частицы может быть описано как совокупность состояний со спином 1 / 2 , ориентированных в произвольных направлениях

В частном случае при n = 1 , как в приведенном выше примере с электроном, мы получим одну точку на сфере Римана. Это — просто точка, помеченная значением q в приведенных выше описаниях. Но для состояний с высшим спином картина, как я только что описал, значительно усложняется, хотя надо заметить, что это описание почему-то не очень знакомо физикам.

В этом описании есть нечто весьма удивительное. Часто высказывают мнение, что в некотором подходящем пределе квантовые описания атомов (или элементарных частиц, или молекул) с необходимостью переходят в классические ньютоновские описания, когда система увеличивается в размерах и усложняется. Но в такой формулировке такое утверждение просто неверно . Ибо, как мы только что видели, спиновые состояния объекта с большим угловым моментом соответствуют большому числу точек, разбросанных по сфере Римана [161]. Мы можем мысленно представлять себе спин объекта как состоящим из целого множества спинов 1 / 2 , ориентированных по всем различным направлениям, задаваемыми этими точками. Лишь весьма немногие из таких комбинированных состояний, а именно когда большинство точек концентрируются вместе в небольшой области на сфере (т. е. когда большинство спинов 1 / 2 направлены примерно в одном и том же направлении), соответствуют реальным состояниям углового момента, которые мы обычно обнаруживаем у классических объектов, например, у крикетных шаров. Мы могли бы ожидать, что если выбрать спиновое состояние, в котором полный спин окажется равным (в единицах ħ / 2 ) некоторому очень большому числу, а в остальном это выбор будет «случайным», то начнет возникать нечто похожее на классический спин. Но в действительности все происходит совсем не так. В общем случае квантовые спиновые состояния с большим полным спином совсем не похожи на классические спиновые состояния!

Как же в таком случае следует устанавливать соответствие с угловым моментом из классической физики? Хотя большинство квантовых состояний с большим спином не похожи на классические состояния, они представляют собой линейные комбинации (ортогональных) состояний, каждое из которых похоже на классическое состояние. Каким-то образом над системой оказывается произведенным «измерение», и состояние «скачком» переходит в то или другое состояние, похожее на классическое. Ситуация здесь аналогична той, которая складывается с любым другим классически измеримым свойством системы, а не только с угловым моментом. Именно этот аспект квантовой механики должен вступать в игру всякий раз, когда система «выходит на классический уровень». Более подробно я расскажу об этом в дальнейшем, но прежде чем мы сможем обсудить такие «большие» или «сложные» квантовые системы, нам необходимо хотя бы несколько разобраться в том странном способе, которым квантовая механика пользуется при рассмотрении систем, состоящих более чем из одной частицы.

Квантовомеханические описания многочастичных состояний, к сожалению, очень сложны. В действительности такие описания чрезвычайно сложны. О них необходимо думать в терминах суперпозиций всех различных возможных расположений всех отдельных частиц! Это приводит к огромному числу возможных состояний — гораздо большему, чем в случае поля в классической теории. Мы уже видели, что квантовое состояние даже одной частицы, а именно волновая функция, обладает сложностями такого рода, которые характерны для всего классического поля. Эта картина (требующая для своего задания бесконечно большого числа параметров) гораздо сложнее, чем классическая картина одной частицы (для задания состояния которой требуется всего лишь небольшое число параметров — точнее, шесть параметров, если частица не обладает внутренними степенями свободы, например, спином; см. главу 5, «Гамильтонова механика»). Такая ситуация может показаться достаточно плохой, и можно было бы думать, что для описания квантового состояния двух частиц понадобится два поля , каждое из которых описывало бы состояние каждой частицы. Ничего подобного! Как мы увидим далее, в случае двух и более частиц описание квантового состояния становится гораздо сложнее.

Квантовое состояние одной (бесспиновой) частицы определяется комплексным числом (амплитудой) для каждого возможного положения, которое может занимать частица. Частица обладает амплитудой, чтобы находиться в точке А, и амплитудой, чтобы находиться в точке В, и амплитудой, чтобы находиться в точке С, и т. д. Подумаем теперь о двух частицах. Первая частица может находиться в точке А, а вторая, например, — в точке В. Возможность такого события должна была бы иметь некоторую амплитуду. С другой стороны, первая частица могла бы находиться в точке В, а вторая — в точке А, и такое расположение частиц также должно иметь некоторую амплитуду; возможно, что первая частица могла бы находиться в точке В, а вторая — в точке Сили, может быть, обе частицы могли бы находиться в точке А. Каждый из этих возможных вариантов должен иметь некоторую амплитуду. Следовательно, волновая функция должна быть не просто парой функций положения (т. е. парой полей), а одной функцией двух положений!

Чтобы получить некоторое представление о том, насколько сложнее задать функцию двух положений по сравнению с двумя функциями положения, представим себе ситуацию, в которой существует лишь конечный набор допустимых положений. Предположим, что разрешены ровно 10 положений, заданных (ортонормированными) состояниями

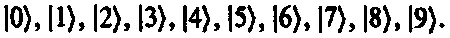
Тогда состояние | φ ) одной частицы было бы какой-то линейной комбинацией

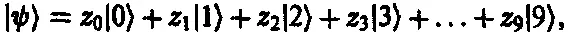
где различные коэффициенты z 0, z 1 , z 2 ,…., z 9 дают, соответственно, амплитуды того, что частица находится попеременно в каждой из 10 точек. Десять комплексных чисел задают состояние одной частицы. В случае двухчастичного состояния нам понадобилось бы по одной амплитуде для каждой пары положений. Всего существуют