Роджер Пенроуз - Новый ум короля: О компьютерах, мышлении и законах физики

10 2 = 100

различных (упорядоченных) пар положений, поэтому нам потребовались бы 100 комплексных чисел! А если бы у нас были только два одночастичных состояния (т. е. «две функции положения», а не «одна функция двух положений», как в приведенном выше примере), то нам понадобилось бы всего лишь 20 комплексных чисел.

Пронумеруем эти 100 комплексных чисел следующим образом

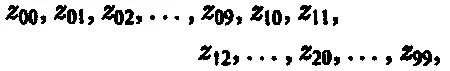
а соответствующие (ортонормированные) базисные векторы [162]

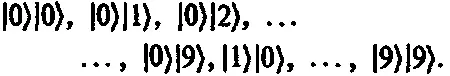
Тогда общее двухчастичное состояние можно было бы представить в виде

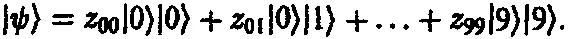
Такое обозначение состояний в виде «произведения» имеет следующий смысл: если | α ) — возможное состояние первой частицы (не обязательно состояние с определенным положением) и если | β ) — возможное состояние второй частицы, то состояние, в котором первая частица находится в состоянии | α ), а вторая — в состоянии | β ), можно представить в виде

| α ) | β ).

«Произведения» можно также брать между любыми другими парами квантовых состояний, а не обязательно между парами одночастичных состояний. Таким образом, мы всегда интерпретируем состояние-произведение | α ) | β ) (не обязательно состояний отдельных частиц) как конъюнкцию

«первая система находится в состоянии | α )» и

«вторая система находится в состоянии | β )»

(Аналогичная интерпретация справедлива и относительно | α ) | β ) | γ ) и т. д.; см. далее.) Однако общее двухчастичное состояние в действительности не имеет вид «произведения». Например, оно может быть представимо в виде

| α )| β ) + | ρ )| σ ),

где | ρ ) — еще одно возможное состояние первой системы,

а | σ ) — еще одно возможное состояние второй системы. Это состояние представляет собой линейную суперпозицию , а именно: суперпозицию первой конъюнкции состояний | α ) и | β ) плюс вторая конъюнкция состояний | ρ ) и | σ ), и не может быть представлено в виде простого произведения (т. е. как конъюнкция двух состояний). Еще один пример — состояние | α )| β ) — | ρ )| σ ) описывало бы другую такую линейную суперпозицию. Заметим, что квантовая механика требует проведения четкого различия между смыслом слов «плюс» и «и». И в обращении с этими словами нам следует быть более осторожными!

В случае трех частиц ситуация во многом аналогична. Чтобы задать общее трехчастичное состояние в приведенном выше примере, где имеются только 10 возможных положений, нам потребовалось бы теперь 1000 комплексных чисел! Полный базис для трехчастичных состояний состоял бы из следующих элементов:

| 0 )| 0 )| 0 ), | 0 )| 0 )| 1 ), | 0 )| 0 )| 2 ), …, | 9 )| 9 )| 9 ).

Частные трехчастичные состояния имели бы вид произведений трех сомножителей

| α )| β )| γ )

(где | α ), | β ) и | γ ) — не обязательно состояния с определенным положением), но для общего трехчастичного состояния нам понадобилось бы построить суперпозицию большого числа состояний типа этих простых «произведений». Соответствующая схема получения общего состояния для четырех и более частиц должна быть очевидна.

До сих пор мы рассматривали случай различимых частиц, когда все частицы: «первая», «вторая», «третья» и т. д. принадлежат к разным типам. Одна из поразительных особенностей квантовой механики заключается в том, что в случае «тождественных» частиц правила коренным образом меняются. Действительно, правила становятся такими, что в самом прямом смысле частицы определенного типа должны быть не просто почти тождественными, а в точности тождественными. Это относится ко всем электронам и ко всем фотонам. Но оказывается, что все электроны тождественны друг другу совсем не так , как тождественны все фотоны! Различие заключается в том, что электроны принадлежат к так называемым фермионам, тогда как фотоны принадлежат к бозонам. Эти два класса частиц надлежит рассматривать весьма различным образом.

Прежде чем я окончательно запутаю читателя этими словесными несуразностями, позвольте мне попытаться объяснить, как действительно следует характеризовать фермионные и бозонные состояния. Правило состоит в следующем. Если | ψ ) — состояние, содержащее некоторое число фермионов определенного типа, то при перестановке любых двух фермионов | ψ ) должно перейти в — | ψ ):

| ψ ) → — | ψ )

Если состояние | ψ ) содержит некоторое число бозонов определенного типа, то при перестановке любых двух бозонов | ψ ) должно перейти в | ψ ):

| ψ ) → | ψ )

Отсюда следует, что никакие два фермиона не могут находиться в одном и том же состоянии . Действительно, если бы какие-нибудь два фермиона находились в одном и том же состоянии, то их перестановка вообще никак не сказывалась бы на полном состоянии системы, следовательно должно было бы выполняться — | ψ )=| ψ ) т. е. | ψ )= 0 , что не допустимо для квантового состояния. Это свойство известно как принцип запрета Паули [163], а его следствия для структуры вещества имеют фундаментальный характер. Действительно, все главные составляющие вещества: электроны, протоны и нейтроны принадлежат к числу фермионов. Не будь принципа запрета, вещество бы просто сколлапсировало!

Вернемся к нашему примеру с 10 положениями и предположим теперь, что у нас есть состояние, состоящее из двух тождественных фермионов. Состояние | 0 )| 0 ) исключается в силу принципа Паули (при перестановке первого множителя со вторым оно переходит в себя вместо того, чтобы переходить в себя со знаком минус). Кроме того, состояние | 0 )| 1 ) также само по себе должно быть исключено, так как при перестановке множителей знак минус не появляется; но это легко можно исправить, если заменить произведение | 0 )| 1 ) комбинацией