Роджер Пенроуз - Новый ум короля: О компьютерах, мышлении и законах физики

Чтобы убедиться в этом, рассмотрим ситуацию, аналогичную изложенной выше, но такую, что выбор измерения , производимого над системой А, остается нерешенным до тех пор, пока системы Aи Bне окажутся пространственно разделенными. Тогда, как представляется, факт выбора измерения мгновенно окажет влияние на поведение системы B! Этот кажущийся парадоксальным «мысленный эксперимент» ( ЭПР-типа) был предложен Альбертом Эйнштейном, Борисом Подольским и Натаном Розеном [1935]. Я опишу его вариант, предложенный Давидом Бомом [1951]. То, что никакое локальное «реалистическое» (т. е. типа скрытых переменных или «классического типа») описание не может дать правильные квантовые вероятности, следует из одной замечательной теоремы Джона С. Белла (Белл [1987], Рэй [1986], Сквайерс [1986]).

Предположим, что две частицы со спином 1 / 2 , которые я буду называть электроном и позитроном (т. е. антиэлектроном ), возникли в результате распада одной частицы со спином 0 в некоторой точке (центре), и что они движутся от центра в противоположных направлениях (рис. 6.30).

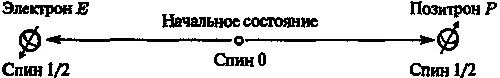
Рис. 6.30.Частица с нулевым спином распадается на две частицы с половинным спином — электрон Б и позитрон Р. Представляется, что измерение спина одной из частиц со спином 1/2 мгновенно фиксирует состояние спина другой частицы

Из закона сохранения углового момента следует, что спины электрона и позитрона в сумме должны давать 0 , так как угловой момент исходной частицы был равен 0 . Отсюда следует, что когда мы измеряем спин электрона в каком-нибудь направлении, то, какое направление мы бы ни выбрали, спин позитрона окажется направленным в противоположную сторону! Электрон и позитрон могут быть разделены расстоянием в несколько миль или даже световых лет, тем не менее кажется, что сам выбор измерения, производимого над одной частицей, мгновенно фиксирует ось спина другой частицы!

Попытаемся теперь выяснить, как квантовый формализм приводит нас к такому заключению. Представим состояние двух частиц с суммарным нулевым угловым моментом вектором состояния | Q ). Тогда имеем соотношение

| Q ) = | E↑) | P↓) — | E↓) | P↑),

где Еозначает электрон, а Р— позитрон. Здесь все описывается в терминах направлений спина «вверх/вниз». Мы видим, что полное состояние является линейной суперпозицией электрона со спином вверх и позитрона со спином вниз, а также электрона со спином вниз и позитрона со спином вверх. Таким образом, если мы измеряем спин электрона в направлении «вверх/вниз» и обнаруживаем, что спин направлен вверх, то мы должны скачком перейти к состоянию | E↑) | P↓), поэтому спиновое состояние позитрона должно быть направлено вниз. С другой стороны, если мы обнаруживаем, что спин электрона направлен вниз, то состояние скачком переходит в | E↓) | P↑), поэтому спин позитрона направлен вверх.

Предположим, что мы выбрали какую-то другую пару противоположных направлений, например, вправо и влево, где

| E→) = | E↑) + | E↓), | P→) = | P↑) + | P↓)

и

| E←) = | E↑) — | E↓), | P←) = | P↑) — | P↓).

Тогда мы находим (если угодно, можете проверить выкладки):

| E→) | P←) — | E←) | P→) = (| E↑) + | E↓) (| P↑) — | P↓) — (| E↑) — | E↓)) (| P↑) + | P↓)) = | E↑)| P↑) + | E↓)| P↑) — | E↑)| P↓) — | E↓)| P↓) — | E↑)| P↑) + | E↓)| P↑) — | E↑)| P↓) + | E↓)| P↓) = - 2 (| E↑)| P↓) — | E↓)| P↑) = - 2 | Q )

т. е. мы получили (с точностью до несущественного множителя - 2 ) то же самое состояние, из которого мы «стартовали». Таким образом, наше исходное состояние можно одинаково хорошо считать линейной суперпозицией электрона со спином вправо, позитрона со спином влево, и электрона со спином влево, позитрона со спином вправо! Выписанное выше выражение полезно, если мы решили измерять спин электрона в направлении вправо-влево вместо направления вверх-вниз. Если мы обнаружим, что спин электрона действительно направлен вправо, то состояние системы скачком переходит в | E→) | P←), поэтому спин позитрона направлен влево. С другой стороны, если мы обнаружим, что спин электрона направлен влево, то состояние системы скачком переходит в | E←) | P→), поэтому спин позитрона направлен вправо. Если бы мы стали измерять спин электрона в любом другом направлении, то получили бы соответствующую ситуацию: спиновое состояние позитрона мгновенно перешло бы скачком либо в измеряемое направление, либо в противоположное направление, в зависимости от измерения спина электрона.

Почему мы не можем моделировать спины наших частиц — электрона и позитрона аналогично тому, как мы поступили в приведенном выше примере с черным и белым шарами, извлекаемыми из ящика? Будем рассуждать на самом общем уровне. Вместо черного и белого шаров мы могли бы взять два каких-нибудь технических устройства Еи Р, первоначально образовывавших единое целое, а затем начавших двигаться в противоположные стороны. Предположим, что каждое из устройств Еи Рспособно давать ответ ДАили НЕТна измерение спина в любом заданном направлении. Этот ответ может полностью определяться технической начинкой устройства при любом выборе направления — или, может быть, устройство дает только вероятностные ответы (вероятность определяется его технической начинкой) — но при этом мы предполагаем, что после разделения каждое из устройств Е и Р ведет себя совершенно независимо от другого .

Поставим с каждой стороны измерители спина, один из которых измеряет спин Е, а другой — спин Р. Предположим, что каждый измеритель обладает тремя настройками для измерения направления спина при каждом измерении, например, настройками А , В , С для измерителя спина Еи настройками А ', В ', С ' для измерителя спина Р. Направления А ', В ', С ' должны быть параллельны, соответственно, направлениям А , В , и С . Предполагается также, что все три направления А , В , и С лежат в одной плоскости и образуют между собой попарно равные углы, т. е. углы в 120 ° (рис. 6.31).