Роджер Пенроуз - Новый ум короля: О компьютерах, мышлении и законах физики

Платоном в Афинах была основана Академия, в задачи которой входило дальнейшее развития таких идей. Среди элиты, выросшей из числа членов этой Академии, был и необычайно влиятельный и знаменитый философ Аристотель. Но здесь нас будет интересовать другой человек, принадлежащий к платоновской Академии — математик и астроном Евдокс, несколько менее известный, чем Аристотель, но, по моему глубокому убеждению, гораздо более проницательный ученый, один из величайших мыслителей античности.

В евклидовой геометрии есть одна очень важная и тонкая составляющая, которая, на самом деле, является очень существенной и которую сегодня мы вряд ли вообще отнесли бы к геометрии! (Математики охотнее назвали бы это «анализом», чем «геометрией».) Речь идет о введении действительных чисел . Евклидова геометрия использует длины и углы. Чтобы иметь возможность использовать такую геометрию, нам необходимо понимать, какого рода «числа» нужны для описания этих самых длин и углов. И здесь новая идея была предложена Евдоксом (ок. 408–335 гг. до н. э.) в IV веке до н. э. [104]) Греческая геометрия переживала «кризис» из-за открытия пифагорейцами таких чисел, как √2 (последнее необходимо для того, чтобы выразить длину диагонали квадрата через длины его сторон), не представимых в виде дроби, т. е. отношения двух целых чисел. Для древних греков было важно иметь возможность формулировать их геометрические меры (отношения) в терминах (отношений) целых чисел, чтобы оперировать геометрическими величинами в соответствии с правилам арифметики. В основном, идея Евдокса заключалась в том, чтобы дать метод описания отношений длин (т. е. действительных чисел!) в терминах целых чисел . Евдоксу удалось сформулировать в рамках операций над целыми числами такие критерии, которые позволяли решать, является ли одно из отношений длин больше другого или их можно считать в точности равными.

В общих чертах идея Евдокса сводится к следующему: если a , b , c и d — четыре длины, то критерием, позволяющим утверждать, что отношение а/b больше отношения c/d , будет существование таких целых чисел М и N , что длина а , сложенная сама с собой N раз, больше длины b , сложенной сама с собой М раз, — тогда как длина d , сложенная сама с собой М раз, больше длины с , прибавленной к самой себе N раз [105]). Соответствующий критерий можно аналогичным образом использовать для установления противоположного неравенства а/b < c/d . А искомый критерий равенства а/b = c/d просто отвечает случаю, когда ни один из двух критериев ( а/b > c/d и а/b < c/d ) не может быть выполнен!

Совершенно точная абстрактная математическая теория действительных чисел была построена только в XIX веке такими математиками, как Дедекинд и Вейерштрасс. Но в действительности, предложенная ими процедура опиралась на те же идеи, которые были открыты Евдоксом примерно двадцатью двумя столетиями раньше! Сейчас нам не обязательно заниматься подробным изучением этой современной теории. Я кратко коснулся ее основных моментов в главе 3 (подглава «Действительные числа»), где для большей наглядности изложения предпочел использовать более привычное десятичное разложение действительных чисел. (В действительности, десятичное разложение была введено Стевином в 1585 году.) Следует также заметить, что хорошо знакомая нам десятичная запись была неизвестна древним грекам.

Однако, между теориями, предложенными Евдоксом с одной стороны, и Дедекиндом и Вейерштрассом — с другой, существует важное различие. Древние греки рассматривали действительные числа как изначально данные — в терминах (отношений) геометрических величин — т. е. как свойства «реального» пространства. Древним грекам было необходимо иметь возможность описывать геометрические величины арифметически, чтобы затем в рамках законов и правил арифметики проводить строгие рассуждения над этими геометрическими величинам, а также их суммами и произведениями — существенными составляющими столь многих замечательных геометрических теорем древних. (На рис. 5.3 в качестве иллюстрации приведена знаменитая теорема Птолемея, хотя Птолемей открыл ее гораздо позже эпохи, в которую жил Евдокс. Теорема Птолемея устанавливает соотношение, которому удовлетворяют расстояния между четырьмя точками на окружности; в ее формулировке с необходимостью используются как понятие суммы, так и понятие произведения.) Критерии Евдокса оказались необычайно плодотворными и, в частности, позволили древним грекам строго вычислять площади и объема.

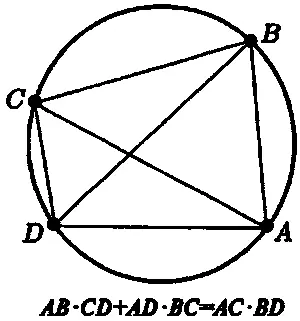
Рис. 5.3.Теорема Птолемея

Но для математиков XIX века — и, разумеется, для современных математиков роль геометрии изменилась. Для древних греков и, в частности, для Евдокса, «действительные» числа были объектами, извлеченными из геометрии физического пространства. Ныне мы предпочитаем считать, что действительные числа логически более первичны, чем геометрия. Это позволяет нам конструировать всевозможные различные типы геометрии, каждый из которых исходит из понятия числа. (Ключевой идеей была идея координатной геометрии, введенная в XVII веке Ферма и Декартом. Координаты можно использовать для определения других типов геометрии.) Любая такая «геометрия» должна быть логически непротиворечивой, но не обязательно должна иметь прямое отношение к физическому пространству нашего эмпирического опыта. Конкретную физическую геометрию мы, по-видимому, постигаем через идеализацию эмпирического опыта (т. е. в зависимости от наших экстраполяций на бесконечно большие или бесконечно малые размеры, — см. главу 3, подглава «„Действительность“ действительных чисел»). Проводимые ныне эксперименты достаточно точны и приводят нас с необходимостью к заключению, что наша «извлеченная из эмпирического опыта» геометрия в действительности отличается от евклидова идеала (см. гл.5, конец подглавы «Общая теория относительности Эйнштейна») и согласуется с геометрией, требуемой в общей теорией относительности Эйнштейна. Однако, несмотря на изменения в наших взглядах на геометрию физического мира, возникших в настоящее время, понятие действительного числа, выдвинутое Евдоксом двадцать три столетия назад, по существу осталось неизменным и является существенным ингредиентом как теории Эйнштейна, так и теории Евклида. В действительности это понятие служит существенным ингредиентом всех современных серьезных физических теорий!