Роджер Пенроуз - Новый ум короля: О компьютерах, мышлении и законах физики

Этот замечательный факт, получивший название принципа относительности Галилея , имеет в действительности решающее значение для наполнения копернианской точки зрения динамическим смыслом. Николай Коперник (1473–1543) и древнегреческий астроном Аристарх (ок. 310–230 гг. до н. э.; не путать с Аристотелем!) за восемнадцать веков до Коперника выдвинули гипотезу о том, что Солнце покоится, а Земля движется, вращаясь вокруг своей собственной оси и обращаясь по орбите вокруг Солнца. Почему мы не ощущаем этого движения, которое происходит со скоростью около нескольких сотен тысяч километров в час? До того, как Галилей выдвинул свою динамическую теорию, этот вопрос действительно представлял настоящую и глубокую загадку для сторонников копернианской картины мироздания. Если бы была верна более ранняя «аристотелевская» версия динамики, согласно которой реальная скорость системы в ее движении сквозь пространство влияла бы на динамическое поведение системы, то движение Земли заведомо было бы чем-то непосредственно очевидным для нас. Относительность Галилея позволяет понять, каким образом Земля может находиться в движении, хотя это движение не будет чем-то воспринимаемым нами непосредственно [107]).

Заметим, что в рамках галилеевой относительности не существует локального физического смысла, который можно было бы придать понятию «в покое». Это приводит к важным следствиям относительно того, как надлежит рассматривать пространство и время. Интуитивная картина пространства и времени состоит в том, что «пространство» представляет собой своего рода арену, на которой происходят физические события. Физический объект может в один момент времени находиться в одной точке пространства, а в более поздний момент времени может оставаться в той же точке или оказаться в другой точке пространства. Представим себе мысленно, что точки пространства каким-то образом могут сохранять свое положение от одного момента времени до следующего момента так, что имеет смысл говорить о том, изменил ли некоторый объект свое положение в пространстве или не изменил. Но галилеева относительность учит нас, что «состояние покоя» не имеет абсолютного характера и поэтому невозможно придать смысл выражению «одна и та же точка пространства в два различных момента времени». Какая точка евклидова трехмерного пространства физической реальности в один момент времени является «той же» точкой евклидова трехмерного пространства в другой момент времени? На этот вопрос невозможно ответить. Создается впечатление, что для каждого момента времени нам необходимо иметь совершенно «новое» евклидово пространство! Этому можно придать смысл, если рассмотреть четырехмерную пространственно-временну́ю картину физической реальности (рис. 5.5).

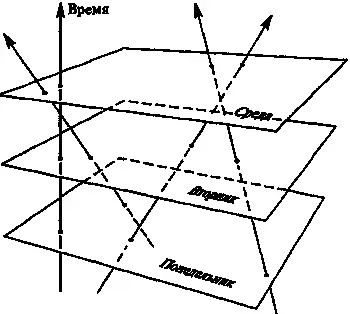
Рис. 5.5.Галилеево пространство-время: частицы, движущиеся равномерно и прямолинейно, изображены в виде прямых

Трехмерные евклидовы пространства, соответствующие различным моментам времени, в этой картине действительно рассматриваются отдельно друг от друга, но все эти пространства объединены, образуя совместно полную картину четырехмерного пространства-времени. Истории частиц, движущихся равномерно и прямолинейно, описываются прямыми (называемыми мировыми линиями) в пространстве-времени. В дальнейшем я еще вернусь к проблеме пространства-времени и относительности движения в контексте эйнштейновской специальной теории относительности. Мы увидим, что довод в пользу четырехмерности обретает в этом случае гораздо бо́льшую силу.

Третья из великих догадок Галилея стала ключом к началу понимания закона сохранения энергии . Галилея главным образом интересовало движение объектов под действием силы тяжести. Он заметил, что если тело стартует из состояния покоя, то идет ли речь о свободно падающем теле, или о колеблющемся маятнике произвольной длины, или о теле, соскальзывающем по наклонной плоскости, скорость движения всегда зависит только от расстояния по вертикали, пройденного телом от начального положения. Кроме того, достигнутая скорость всегда в точности достаточна для возвращения тела на ту высоту, с которой оно начало двигаться. Теперь мы должны были бы сказать, что энергия, запасенная телом на исходной высоте над поверхностью земли (гравитационная потенциальная энергия), может превращаться в энергию движения тела (кинетическую энергию, которая зависит от величины скорости тела ), а та, в свою очередь, — в потенциальную энергию, причем в целом энергия не утрачивается и не приобретается.

Закон сохранения энергии — очень важный физический принцип. Это — не независимое физическое требование, а следствие из законов движения Ньютона, до которых мы скоро дойдем. На протяжении столетий все более понятные формулировки закона сохранения энергии делались Декартом, Гюйгенсом, Лейбницем, Эйлером и Кельвином. Позднее в этой главе и в главе 7 мы еще вернемся к закону сохранения энергии. Оказывается, что в сочетании с галилеевским принципом относительности закон сохранения энергии приводит к другим законам сохранения, имеющим немалое значение: закону сохранения массы и закону сохранения количества движения ( импульса ). Количество движения частицы равно произведению ее массы и ее скорости. Знакомые примеры сохранения количества движения возникают при рассмотрении реактивного движения, когда увеличение направленного вперед количества движения ракеты в точности уравновешивается направленным назад количеством движения выхлопных газов (обладающих меньшей массой, но зато большей скоростью). Отдача ружья при выстреле — еще одно проявление закона сохранения количества движения. Еще одним следствием из законов движения Ньютона служит закон сохранения углового момента ( момента количества движения ), описывающий постоянство вращения системы вокруг собственной оси. Вращение Земли вокруг собственной оси, равно как и вращение теннисного мяча вокруг собственной оси, не затухают благодаря закону сохранения их угловых моментов. Каждая частица, образующая любое тело, вносит свой вклад в полный угловой момент тела, причем величина этого вклада равна произведению количества движения частицы на расстояние ее от оси вращения (длину перпендикуляра, опущенного из точки, где находится частица, на ось вращения). (Следовательно, угловую скорость свободно вращающегося объекта можно увеличить, сделав объект более компактным. Это приводит к поразительному, но хорошо знакомому действию, часто исполняемому спортсменами на льду и воздушными гимнастами на трапеции. Прижав к себе руки или поджав ноги, они резко увеличивают скорость вращения просто вследствие закона сохранения углового момента!) Как будет показано в дальнейшем, масса, энергия, количество движения (импульс) и угловой момент принадлежат к числу важных для нас понятий. Наконец, мне следовало бы напомнить читателю о пророческой догадке Галилея, понявшего, что в отсутствие атмосферного сопротивления все тела под действием силы тяжести падают с одной и той же скоростью. (Возможно, читатель вспомнит известную легенду о том, как Галилей сбрасывал с наклонной башни в Пизе по несколько предметов одновременно.) Три столетия спустя то же самое озарение привело Эйнштейна к обобщению принципа относительности на ускоренные системы отсчета и стало, как мы увидим в конце этой главы, краеугольным камнем его необычайной общерелятивистской теории относительности.