Александр Петров - Гравитация. От хрустальных сфер до кротовых нор

Теперь вернемся к понятию космологической сингулярности, мыслимой как некая исходная «точка». Поскольку какого-то выделенного центра нет, ее нельзя представить как «точку», помещенную в какое-то внешнее пространство. Это объект «сам по себе» и содержащий в себе еще не возникшие пространство и время. Здесь, конечно, речь о внешнем пространстве той же размерности, что и наша Вселенная. Тогда, давайте, поместим нашу Вселенную («точку») в пространство большей размерности, и там ее «взорвем», как бомбу. Но при этом необходимо признать, что должно быть воздействие внешнего пространства на наше внутреннее и наоборот. Пока такого

«взаимодействия» не зарегистрировано, хотя очень активно возможности его проявления и анализируются, и проводятся соответствующие эксперименты. Кроме того, если мы разлетаемся из-за «реального» взрыва в пространстве большей размерности, то в раннюю эпоху его влияние на нашу Вселенную должно было быть чрезвычайным, и это влияние должно было бы оставить след. Но как показывают космологические исследования, нет необходимости привлекать такого рода экзотические силы, чтобы объяснять явления ранней Вселенной.

Наличие сингулярности в теории долгие годы вызывало и вызывает активную критику. Действительно, смещаясь назад по времени, исследователь достигает таких огромных значений физических характеристик, при которых физика явлений просто неизвестна. Поэтому говорить, что расширение началось с сингулярности, строго говоря, нельзя. Что служит разумным ограничением для предельных значений? С построением квантовой механики к двум основным физическим постоянным, о которых мы уже говорили – гравитационной G ≈ 6,67 · 10 –8см 3/г·с 2и скорости света с ≈ 3 · 10 10см/с, добавилась третья – постоянная Планка h ≈ 3,32 · 10 –27г · см 2/с = 3,32 · 10 –34Дж · с. С их помощью, с использованием всех трех, стало возможным построение любой физической величины любой размерности, а значение такой величины получило название планковской. Таким образом, планковские масштаб и время имеют значения l ~ 10 –33см и t ~ 10 –43с. Существуют также планковские плотность, давление и т. д.

Современная физика не может определенно сказать, что происходит на масштабах и в промежутки времени меньше планковских, или при плотностях, давлениях и т. д. – больше планковских. Таким образом, обычно историю развития Вселенной начинают исследовать с некоторого сверхплотного «зародыша», имеющего планковские характеристики. Конечно, вопрос появления самого «зародыша» есть и будет предметом дальнейших исследований.

Например, на основе тех же квантовых представлений при некоторых предположениях предлагаются модели рождения «из ничего». Их основное содержание в том, что Вселенная начинает развиваться из квантовой флуктуации. Важно отметить, что именно модели Фридмана с замкнутым пространством оказываются более подходящими для сценариев квантового рождения Вселенной. Подробнее об этой возможности мы поговорим в главе о гравитационной энергии.

Подведем некоторый итог. Конечно, понятие «Большой взрыв» принципиально отличается от обычных взрывов. Кроме того, это не одномоментное явление, которое происходит в виде разлета начальной сингулярности, а, скорее, самый ранний период в истории Вселенной, который начинается с планковских масштабов.

Вернемся к парадоксам нерелятивистской космологии. Вспомним, что причина гравитационного парадокса в том, что для однозначного определения гравитационного воздействия либо недостаточно уравнений, либо нет возможности корректно задать граничные условия. В случае фридмановской космологии независимыми являются два уравнения Эйнштейна. Учитывается также уравнение состояния (связи между плотностью и давлением). Кроме того, на данный момент времени из наблюдений известны плотность и скорость расширения.

Все это однозначно определяет эволюцию масштабного фактора a ( t ), плотность ρ и давление p. Становится известной геометрия космологического пространства-времени, а значит, тип и динамика 3-мерного пространства, в котором звезды, галактики, скопления галактик ведут себя в соответствии с современными наблюдениями. То есть гравитационного парадокса не возникает.

Теперь зададимся, возможно, провокационным вопросом. А можно ли описать расширяющуюся Вселенную с помощью гравитации Ньютона? Оказывается, можно! Обратимся к опыту Зельдовича. В своих лекциях он всегда старался представить материал простейшим способом, а рассказывая о космологических решениях, по возможности ограничивался теорией Ньютона.

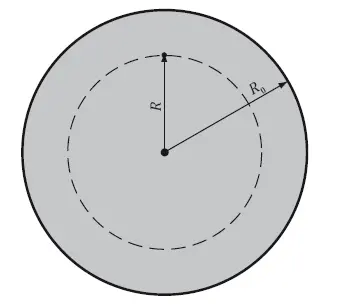
Рис. 9.4. Схема расчета ускорений

Рассмотрим шар радиуса R 0и элемент массы m внутри шара на расстоянии от центра R < R 0(рис. 9.4). Такая задача рассматривалась еще Ньютоном. Он же и установил, что сила, действующая на m , определяется массой материи внутри сферы радиуса R , а гравитационное действие внешних областей взаимно компенсируется:

F = GMm / R 2,

здесь: M = (4π/3) R 3ρ – масса материи внутри сферы, ρ – плотность материи, распределенная однородно. Следовательно, ускорение

a = (4π/3) G ρ R = CR .

Таким образом, ускорение элемента в точке R пропорционально его расстоянию от центра и не зависит от радиуса шара R 0при любом, сколь угодно большом R 0. Это фактически означает, что соотношение справедливо для бесконечной однородной вселенной.

Но остается вопрос: решение было найдено для некоторого центра, в котором ускорение равно нулю, а в других точках имеет вполне определенную величину и направлено к центру. А где такой центр в бесконечной однородной вселенной? На самом деле, никакого выделенного центра нет или, если угодно, таким центром может быть любая точка. Возьмем произвольную точку О′ , находящуюся на некотором расстоянии R О′ от «нашего» центра, ускорение которой a О′ = – С R О′ . Радиус-вектор и ускорение направлены, разумеется, в разные стороны. Перейдем в систему координат с центром в точке О′ (рис. 9.5). Величины в этой новой системе координат будем обозначать штрихом.

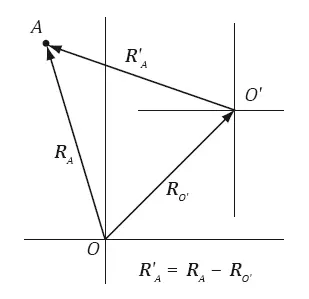
Рис. 9.5. Переход к другой системе координат

Ускорения в старой и новой системах координат связаны правилом Галилея, которое, если кто забыл, справедливо не только для скоростей, но и для ускорений: