Майкл Файер - Абсолютный минимум. Как квантовая теория объясняет наш мир

Для молекул ароматических соединений квантовая теория позволяет рассчитать молекулярные орбитали, а также их формы и размеры. Есть много способов проверить результаты квантовых вычислений путём сравнения с данными экспериментов. Один из наиболее полезных способов состоит в применении оптической спектроскопии для измерения длин волн (цветов) света, поглощаемого молекулами. Рассмотрим в качестве примера нафталин.

На рис. 18.7 представлена молекулярная диаграмма нафталина, содержащего десять атомов углерода. Каждый атом углерода вносит одну p z-орбиталь с одним электроном в образование делокализованной системы π-электронов. Ещё три валентных электрона каждого атома углерода служат для образования σ-связей. Десять атомных p z-орбиталей образуют π-систему, в которой, таким образом, будет десять молекулярных орбиталей: пять связывающих и пять разрыхляющих. В нафталине нет вырожденных МО, каждая имеет свою энергию. На рис. 18.9 схематически изображены энергетические уровни π-МО нафталина. Слева показаны энергетические π-уровни с десятью π-электронами, заполняющими пять связывающих МО. Разрыхляющие МО пустуют.

На рис. 18.9 показан эффект поглощения света. Поскольку энергетические уровни квантуются, молекула может поглощать свет лишь с определёнными значениями энергии. На рисунке ∆ E — наименьшая энергия света, который может быть поглощён. Рассмотрим, что случится, если направить свет на образец с молекулами нафталина, начиная со света, который имеет слишком низкую энергию, чтобы быть поглощённым молекулами. Энергия света описывается формулой E = h∙ ν , где h — постоянная Планка, а ν — частота. Итак, первоначально ∆ E > h∙ ν , то есть разница в энергии между верхней занятой молекулярной орбиталью (ВЗМО) и нижней свободной молекулярной орбиталью (НСМО) больше энергии фотонов, проникающих в образец. В результате они пройдут сквозь образец без поглощения. Теперь начнём изменять энергию света, повышая её (от красного к голубому). Когда h∙ ν =∆ E , свет поглощается, что проявляется в уменьшении количества излучения, проходящего сквозь образец. Электрон возбуждается, переходя с НСМО на ВЗМО. Это возбуждение показано в правой части рис. 18.9, где один электрон находится на ВЗМО и один электрон — на НСМО. В левой части рис. 18.9 на ВЗМО находятся два электрона, а на НСМО — ни одного.

Переход с ВЗМО на НСМО — это энергетически наименее затратный переход. Из рисунка видно, что связывающие МО находятся друг к другу ближе, чем ВЗМО и НСМО. Однако электрон не может возбудиться, перейдя с одной заполненной связывающей МО на другую. Если попытаться забрать электрон с одной связывающей МО и поместить его на другую, то получится МО с тремя электронами. Три электрона на МО нарушают принцип запрета Паули. Поэтому в нашем оптическом эксперименте, в котором цвет излучения меняется от красного к голубому (от низкой энергии к высокой), первым цветом (длиной волны), который подвергается поглощению, будет тот, что соответствует энергии ∆ E . Значение ∆ E можно вычислить на основе квантовой механики. Оно зависит от строения молекулы и взаимодействия атомных орбиталей, которые образуют молекулярные орбитали. Результаты квантовых вычислений в дальнейшем можно проверить, сравнивая с длинами волн, при которых будет происходить поглощение, по мере увеличения энергии света, смещающегося по спектру всё ближе к голубому. Второй раз поглощение произойдёт, когда свет сможет поднять электрон с ВЗМО на энергетический уровень, находящийся выше НСМО. Следующее поглощение соответствует переходу электрона с ВЗМО на орбиталь, которая на два энергетических уровня выше НСМО, и т. д.

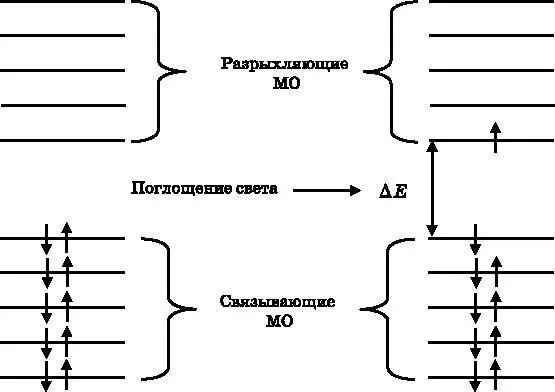
Рис. 18.9. Схема энергетических уровней молекулярных π- орбиталей нафталина. Имеются пять связывающих и пять разрыхляющих МО. Слева изображены десять π- электронов, заполняющих пять связывающих МО. Справа показан результат поглощения света: один из электронов увеличил свою энергию и поднялся на разрыхляющую МО

С помощью современной квантовой теории и компьютеров строение нафталина можно рассчитать с высокой точностью. Теория даёт значения длины связей и угла между ними. Например, длину связей можно вычислить с точностью до 0,001 нм, то есть до тысячной доли нанометра. На основе результатов этих вычислений можно также с высокой точностью рассчитать частоты, на которых поглощается свет. В вычислениях используются значения массы, числа электронов и заряда ядер. Расчёты охватывают как σ-, так и π-связи. Как уже говорилось, π-электроны не локализованы у одного или двух центров атомов углерода, а размазаны по всей углеродной структуре молекулы. Наименьшая энергия поглощения для нафталина, соответствующая переходу с ВЗМО на НСМО, характеризуется длиной волны 320 нм , которая лежит в ультрафиолетовой части оптического спектра.

Можно грубо рассчитать её, рассматривая π-электроны как частицы в ящике. В главе 8 задача о частице в ящике описывалась во всех подробностях. Если рассмотреть переход с ВЗМО на НСМО как переход электрона в ящике с уровня n =1 на уровень n =2 (см. рис. 8.7), то можно воспользоваться формулами, выведенными сразу после рис. 8.7. Для этого перехода получаем

∆ E =3 ∙h 2/8 ∙m∙L 2,

где h — постоянная Планка, m — масса электрона, а L — длина ящика. Здесь мы примем значение L равным 0,51 нм , то есть поперечнику углеродной структуры нафталина. Тогда

∆ E = 3∙(6,6∙10 −34) 2/8∙(9,1∙10 −31)∙(0,8∙10 −9) 2= 6,9∙10 −19.

Преобразовав эту энергию в частоту путём деления на h , получаем: ν =1,04∙10 15 Гц . Тогда длина волны поглощаемого света составит: λ =2,87∙10 −7 м = 287 нм . Эта длина волны лежит дальше в ультрафиолетовой области, чем реальная, но всё же она не очень далека от наблюдаемого значения.

Расчёт для частицы в ящике показывает, что если частица с массой электрона заключена в ящике размером с молекулу нафталина, то первая линия поглощения будет находиться в ультрафиолетовом диапазоне. Удовлетворительная точность, полученная для нафталина при расчёте по модели частицы в ящике, представляет собой до некоторой степени случайную удачу. Даже если моделировать нафталин как частицу в ящике, это должен быть двух- или трёхмерный ящик, а не одномерный. Подобные расчёты обычно приводят к существенным ошибкам. Однако точные квантовомеханические вычисления позволяют определить строение молекулы и значительно более точные частоты поглощения света. Кроме того, если, например, заменить водород фтором, то квантовая теория точно предскажет, насколько изменятся частоты поглощения света фторнафталином по сравнению с обычным нафталином.