Майкл Файер - Абсолютный минимум. Как квантовая теория объясняет наш мир

Волны, у которых сдвиг по фазе составляет 180°, тоже могут складываться друг с другом. Как показано в левой части рис. 3.3, у таких волн положительные пики верхней волны в точности совпадают с отрицательными пиками нижней волны, и наоборот {6} 6 О таких волнах говорят, что они находятся в противофазе. — Примеч. пер. . (И вновь подчеркнём: для того чтобы имела место интерференция, волны должны в действительности накладываться одна на другую, но на рисунке они сдвинуты по вертикали одна относительно другой, чтобы их можно было разглядеть.) Штриховая вертикальная линия на рисунке показывает, что положительный пик одной волны в точности выровнен относительно отрицательного пика другой. Когда две одинаковые волны, находящиеся в противофазе, складываются, положительные и отрицательные пики в точности гасят друг друга. Пусть, например, максимальное положительное значение — +1, а максимальное отрицательное значение составляет −1. Складывая +1 и −1, получаем ноль.

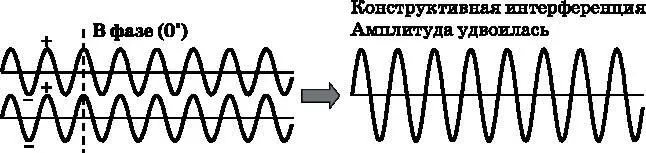
Рис. 3.2. Две одинаковые волны, находящиеся в фазе друг с другом. Эти волны испытывают положительные и отрицательные колебания относительно нуля (горизонтальная линия). Положительные пики выровнены друг относительно друга, как и отрицательные пики. Волны испытывают конструктивную интерференцию (складываются друг с другом) и порождают волну с удвоенной амплитудой

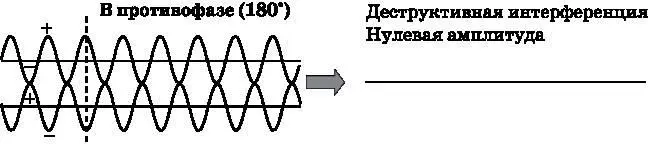
Рис. 3.3. Две одинаковые волны, сдвинутые на 180° по фазе. Эти волны испытывают положительные и отрицательные колебания относительно нуля (горизонтальная линия). Положительные пики верхней волны строго выровнены с отрицательными пиками нижней волны, а отрицательные пики верхней волны строго выровнены с положительными пиками нижней волны. Волны испытывают деструктивную интерференцию, когда складываются друг с другом и дают нулевую амплитуду

На рис. 3.3 каждой точке верхней волны, имеющей положительное значение, строго соответствует точка нижней волны, имеющая такое же по абсолютной величине отрицательное значение, а каждой точке верхней волны, имеющей отрицательное значение, соответствует точка нижней волны, имеющая такое же по абсолютной величине положительное значение. Таким образом, волны в точности гасят друг друга, давая нулевую амплитуду, как показано в правой части рисунка. Это взаимное гашение называется деструктивной интерференцией.

Для интерференции волнам не обязательно строго накладываться друг на друга и идти в одном направлении. Они могут просто перекрываться в некоторой области пространства, и тогда интерференция происходит в этой области. Когда в 1980 году в Сан-Франциско открылся симфонический концертный зал Дэвиса, в нём обнаружились акустические проблемы. Хотя они оказались крайне сложными, нетрудно понять, как они возникли.

Представьте, что вы сидите в зале достаточно далеко от оркестра. Когда звучит ля первой октавы (440 Гц ), акустические волны приходят прямо к вам, но они также отражаются от стен с обеих сторон от вас. При наличии отражения от стены справа от вас и отражения от стены слева от вас отражённые акустические (звуковые) волны от каждой стены приходят к вашему ряду кресел, скажем, под углом 30° и порождают вдоль него интерференционную картину. Будут места, где отражённые волны интерферируют конструктивно, делая звук громче, и места, где волны интерферируют деструктивно, делая звук тише. Интервалы между пиками и нулями интерференционной картины составляют 0,73 м (см. ниже формулу для интервалов). Таким образом, в зависимости от расположения вашего кресла ля первой октавы будет звучать громче или тише. Конечно, к вам приходит множество акустических волн разной частоты с разных направлений. Совокупность интерференционных эффектов искажает звук, который должен был приходить к вам прямо от оркестра. Проблемы в концертном зале Дэвиса были устранены в 1992 году путём установки 88 тщательно спроектированных панелей, свисающих с потолка вдоль двух боковых стен. Там нет двух одинаковых панелей. Они заполнены песком и весят 3850 кг . Эти панели мешают отражениям от стен доходить до аудитории.

Свет также может демонстрировать явление интерференции. Классическое представление об оптических интерференционных картинах позволяет объяснить экспериментальные результаты, которые мы сейчас рассмотрим. Однако, как будет показано в главах 4 и 5, классическое описание в итоге оказывается несостоятельным, когда в расчёт принимаются другие эксперименты. Для корректного описания потребуется ввести квантовомеханический принцип суперпозиции, что вновь приведёт нас к котам Шрёдингера.

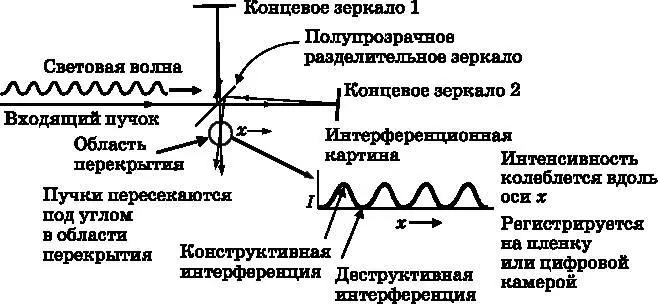
Рис. 3.4. Входящая световая волна падает на полупрозрачное зеркало. Половина света проходит сквозь зеркало, а половина отражается от него. В каждом плече интерферометра свет отражается от стоящего в конце зеркала. Части каждого пучка сходятся под небольшим углом в области перекрытия. Справа от обведённой кружком области перекрытия в увеличенном масштабе в разрезе по xпоказано, что видно там при пересечении двух пучков. Именно в этом месте возникает интерференционная картина, в которой интенсивность периодически меняется вдоль оси xот максимального значения до нуля

На рис. 3.4 представлена схема интерферометра, использованного Майкельсоном (Альберт Абрахам Майкельсон, 1853–1931) в его исследованиях природы световых волн. Майкельсон получил в 1907 году Нобелевскую премию по физике

«за создание точных оптических инструментов, а также спектроскопические и метрологические исследования, выполненные с их помощью».

Майкельсон со своим коллегой Морли {7} 7 Эдвард Уильямс Морли (1838–1923) — американский физик и химик, с высочайшей точностью определивший атомную массу кислорода. — Примеч. пер. использовали интерферометр в попытке выяснить природу среды, в которой распространяются световые волны. Водяные волны движутся по воде. Звуковые волны — в воздухе. Эксперимент Майкельсона-Морли показал, что световые волны для своего распространения не нуждаются в среде, которую называли эфиром. Свет распространяется в вакууме. Не существует никакого эфира, заполняющего пространство. Световые волны, приходящие к нам от звёзд, не нуждаются в какой-либо среде, подобно океанским и звуковым волнам, которые представляют собой колебания воды и воздуха соответственно. Это был важный шаг в понимании того, что световые волны не являются волнами в том же самом смысле, что звуковые волны. Здесь же мы хотим лишь понять классическое описание того, что наблюдается с помощью интерферометра.