Joaquin Sandalinas - До предела чисел. Эйлер. Математический анализ.

В 1772 году Эйлер доказал, что число M 31простое. Любопытно, что прошло более 100 лет, прежде чем было найдено следующее простое число — M 127. Сделал это французский математик Эдуард Люка (1842-1891) в 1876 году. Также простыми являются M 61и M 89, но они были открыты позже. Таким образом, на протяжении 104 лет Эйлеру принадлежал рекорд по открытию самого большого простого числа.

Квадратичный закон взаимности, превосходно сформулированный Гауссом в его Disquisitiones arithmeticae ("Арифметические исследования"), появился у Лежандра и Эйлера, который рассказал о нем Гольдбаху в письме 1742 года. Для начала определим, что такое символы Лежандра (p/q).

Предположим, что p и q — разные простые нечетные числа и

(p/q) =

0, если р ≡ 0 (mod q)

1, если х 2≡ р (mod q) разрешимое уравнение

-1, если х 2≡ p (mod q) неразрешимое уравнение.

Таким образом, Гауссу, а не Эйлеру, удалось доказать, что

(p/q) =

(q/p), если q ≡ 1 (mod 4)

(-q/p), если q ≡ 3 (mod 4)

Это можно выразить, хотя это и непросто, в одной формуле. Гаусс сделал это открытие в 19 лет и так гордился им, что назвал его aurum theorema — "золотой теоремой".

Делитель d произвольного числа n называется собственным делителем n, если 1 ≤ d < n. Число n — несобственный делитель n. Первое серьезное исследование Эйлера в области дружественных чисел относится к 1747 году. Два числа считаются дружественными, если сумма собственных делителей одного равна другому и наоборот. Это арифметическое понятие "дружбы" можно проиллюстрировать следующим примером. Возьмем числа 220 и 284. Собственными делителями 220 будут 1, 2, 4, 10,11,20,22,44,55 и 110; а 284 -1,2,4,71 и 142. Получаем, что

220 =1 + 2 + 4 + 10+11+20 + 22 + 44 + 55 + 110 = 284

284 = 1 +2 + 4 + 71 + 142 = 220.

Научная жизнь Лежандра (1752- 1833) началась под счастливой звездой. Он обладал выдающимися интеллектуальными способностями и достаточным состоянием, чтобы посвятить себя работе, ни на что не отвлекаясь. Успехов в математике Лежандр добился не сразу. Вместе с Лапласом он сделал важные разработки в области астрономии, открыв многочлены, позже названные многочленами Лежандра, зашел на малоизвестную территорию эллиптических функций и теории чисел, в рамках которой ему удалось, как он считал, решить старую задачу о квадратичном законе взаимности. Но в его исследовании были ошибки, как впоследствии установил Карл Фридрих Гаусс. За свои астрономические работы Лежандр был принят в члены Лондонского королевского общества. Он также участвовал в работе комиссии по созданию десятичной метрической системы, входившей в программу всеобщей рационализации, начатой после Французской революции. Хотя Лежандр и разделял многие революционные идеи, в эпоху Террора он был вынужден скрываться и потерял свое состояние. После этого он переписал и издал "Начала" Евклида с точки зрения того времени и современным языком, получив оглушительный и долгий успех у читателей. Придя к власти, Наполеон сразу же взял Лежандра под свою протекцию. Ученый, бывший к тому времени уже известным академиком, занялся изучением движения комет, разработал метод наименьших квадратов для вычисления траекторий, опередив на сей раз Гаусса. К этому же периоду относятся его исследования по распределению простых чисел, которое, как он предположил, подчинялось асимптотическому закону:

Это значение, очень близкое к современному, впоследствии совпало с фундаментальной теоремой о распределении простых чисел. Гаусс здесь оказался первым, но он так и не опубликовал свои результаты.

Джон Непер (1550-1617) может по праву считаться изобретателем логарифмов. Он нарисовал две прямые линии следующим образом: на первой отложил отрезок с концами А и В, а параллельно ему провел прямую из точки А'. Затем он предположил, что есть некое тело, которое скользит по бесконечной прямой с постоянной скоростью. В каждой точке X' на прямой он отмечал соответствующую точку на отрезке АВ, но не случайным образом: X двигался со скоростью, равной расстоянию ХВ. Взяв х = ВХ и у = А'Х', Непер создал свой логарифм:

у - logx.

Непер взял AB - 10 7, что привело его к довольно сложным алгебраическим равенствам. Если N — число, a L — логарифм, то Непер вычислил N = 10 7(1-10 -7) L. Мы получаем

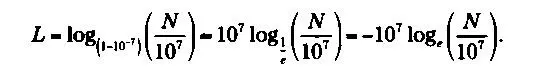
Здесь уже появляется постоянная е, так как

(1 - 10- 7)10 7 ≈1/e.

Во многих старинных трактатах говорится о логарифмах Непера, или натуральных. Здесь мы имеем дело с путаницей, потому что натуральные логарифмы — это логарифмы по основанию е, в то время как все (почти) логарифмы Непера имеют основание 1/е. Это почти одно и то же, они различаются лишь знаком, а не абсолютным значением:

log eN = -log 1/eN.

Сегодня для каждого положительного вещественного числа N, когда N - a L, мы говорим, что L — логарифм N по основанию а, и записываем: L = log aN.

Если мы задумаемся, то увидим, что логарифм основания всегда равен 1, и это его основополагающее свойство.

Самые распространенные основания — это а = 10,а = 2 и а- = е. Логарифмы по основанию 10 называются десятичными, по основанию 2 — двоичными, по основанию е — натуральными. Для натуральных логарифмов используется знак InN вместо log N.

Важным аспектом логарифма является то, что с его помощью упрощаются арифметические вычисления. Например:

Ν 1· Ν 2= a L 1· a L 2= a L 1+L 2

⇒ log a(N 1· N 2) = L 1+ L 2= log aN 1+ log aN 2.

Таким образом, логарифм произведения равен сумме логарифмов его множителей.

Если мы сделаем таблицу с двумя величинами, числами и десятичными логарифмами, то сможем сложить логарифмы и при помощи таблиц легко узнать произведение. И хотя сегодня можно без труда произвести умножение электронными калькуляторами, во времена, когда они еще не существовали, операция, помогающая заменить сложные расчеты в случаях произведений больших величин на простое сложение, имела огромное практическое значение.

Проследим за хитроумными рассуждениями Эйлера, но не будем забывать, что в некоторых местах они должны быть доработаны. Позже это сделал сам ученый. Возьмем знаменитый ряд Тейлора:

sinx = x - x 3/3! + x 5/5! - x 7/7! + ...

Мы знаем, что он равен нулю при х равном нулю, то есть если sinx = 0, когда х = 0, ± π, ±2π, ±3π...

Следовательно, предположив, что ряд ведет себя как многочлен, поскольку он и является длиннейшим многочленом, применение фундаментальной теоремы алгебры преобразит его в произведение одночленов вида х - α, где α — решение. Продолжим: