Joaquin Sandalinas - До предела чисел. Эйлер. Математический анализ.

x - x 3/3! + x 5/5! - x 7/7! + ... = K(x)(x - π)(x + π)(x - 2π)(x + 2π)...

К — неизвестная константа. Производя вычисления в правой части равенства:

x - x 3/3! + x 5/5! - x 7/7! + ... = K(x)(x 2- π 2)(x 2- 4π 2)(x - 9π 2)...

следует отметить, что каждый член вида х 2- λ 2π 2справа равен нулю. А это происходит, только если

1 - х 2/(λ 2π 2) = 0.

Запишем члены правого выражения в следующей форме:

x - x 3/3! + x 5/5! - x 7/7! + ... = K(x)(1 - x 2/π 2)(1 - x 2/4π 2)(1 - x 2/9π 2)...

Теперь разделим на x:

sinx/x = 1 - x 2/3! + x 4/5! - x 6/7! + ... = K(1 - x 2/π 2)(1 - x 2/4π 2)(1 - x 2/9π 2)...

И, поскольку lim x→0(sinx/x) = 1, получим, что K = 1. Итак:

1 - x 2/3! + x 4/5! - x 6/7! + ... = (1 - x 2/π 2)(1 - x 2/4π 2)(1 - x 2/9π 2)...

Этот ряд равен бесконечному произведению. Для Эйлера это не проблема. Подсчитаем порядок произведения и выделим члены произведения с x 2в правой части:

- x 2/3! = -x 2/π 2- x 2/4π 2- x 2/9π 2- ...

Разделив обе части на -x 2/π 2, получим

π 2/6 = 1+ 1/2 2+ 1/2 3+ 1/4 2+ ...,

что и требовалось доказать.

Эйлер был первым математиком, доказавшим тождественность ζ($) как ряда степеней и ζ($) как бесконечного произведения. Назовем р кпростое число, занимающее место k в ряде. Получим

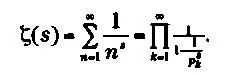
Ниже можно увидеть, каким образом получается это равенство:

Для тех, кто знаком со сложным анализом, дзета-функция может быть расширена до мероморфной во всей комплексной области с простым полюсом s = 1, где остаток равен 1. Это дзета-функция, о которой говорил Риман и которая стала предметом его знаменитой гипотезы.

Чтобы упростить, насколько это возможно, наше объяснение, оттолкнемся от предположения, что задействованные в нем функции удовлетворяют всем необходимым условиям на производную и непрерывность.

Обозначим через S функционал (функцию функций), к которому мы применим вариационное исчисление, а через x 1,х 2— экстремумы неизвестной функции:

S(ƒ) = ∫ x1 x2L(x 1,ƒ(x),ƒ'(x))dx.

Предположим, что решением является ƒ 0и что функционал имеет здесь минимум; назовем α(x) функцию (которую мы будем "варьировать"), равную нулю в экстремумах x1, х 2. Поскольку в ƒ 0функционал имеет минимум,

S(ƒ 0)≤S(ƒ 0+εα)

в окрестности ƒ 0. Вариационный размах

ƒ = ƒ 0+ εα

должен удовлетворять:

dS(ƒ 0+ εα)/dε|ε=0 = ∫ x1 x2dL/dε| ε=0= 0

Теперь вспомним, что

dƒ/dε = α,dƒ'/dε = α'.

Применим правило дифференцирования и проведем необходимые замены.

Получим

dL/dε = ∂L/∂ƒ dƒ/dε + ∂L/∂ƒ' dƒ'/dε = (∂L/∂ƒ)α + ∂L/∂ƒ'α'

A теперь проинтегрируем по частям и учтем предыдущую формулу:

Поскольку выражение слева — ноль, то нулем будет и выражение справа. Следовательно,

dL/dƒ = d/dx ∂L/dƒ' = 0

Таким образом, мы получили уравнения Эйлера — Лагранжа, которые в приложениях обычно приводят к дифференциальным уравнениям второго порядка.

5. КОМПЛЕКСНЫЕ ЧИСЛА

Эйлер вывел свою фундаментальную формулу, из которой впоследствии получил еще несколько из простых рядов Тейлора. Напомним, что степени ведут себя так:

i0 = 1,i1 = i,i2 = -1,i3 = -i,

i 4- 1, i 5= i, i 6= 1,i7 = i и так далее.

Напомним также, что ряды степеней е и тригонометрических функций синус и косинус раскладываются в ряд Тейлора или степенной ряд следующим образом:

ex = x 0/0! + x 1/1! + x 2/2! + x 3/3! + x 4/4! + ...

cosx = x 0/0! + x 2/1! + x 4/4! + x 6/6! + ...

sinx = x 1/1! + x 3/3! + x5/5! + x 7/7! + ...

Произведем вычисления:

e ix= (iz) 0/0! + (iz) 1/1! + (iz) 3/3! + (iz) 4/4! + (iz) 5/5! + (iz) 6/6! + (iz) 7/7! + (iz) 8/8! + ... = z 0/0! + i(z 1/1!) + z 2/2! + i(z 3/3!) + z 4/4! + i(z 5/5!) + z 6/6! + i(z 7/7!) + z 8/8! + ... = (z 0/0! + z 2/2! + z 4/4! + z 6/6! + z 8/8! + ...) + i(z 1/1! + z 3/3! + z 4/4! + z 6/6! + z 8/8! + ...).

Пусть М — сообщение, а С — зашифрованное сообщение (или криптограмма). Предположим, что оба они — натуральные числа. Обозначим через ƒ функцию, которая преобразует М в С: ƒ(M) = С. Чтобы зашифровать М, выбирают два очень больших простых числа, р и q, и определяют модуль, который мы назовем n, так что n = pq и n > М. Выберем такое е, что 1 < е < φ(n), а е и φ(n) взаимно простые числа. Открытый ключ состоит из n и е, и он всем известен. Поскольку n — очень большое число, узнать значение р и q невозможно. Мы имеем E = ƒ(M) ≡ M e(mod n). Назовем закрытым ключом пару n, d, где d выбрано так, что de ≡ 1 (mod φ(n)). Поскольку ρ и q — простые числа, a pq = n, получим, что φ(n) = (р - 1)(q - 1); если мы не знаем p и q, а узнать их фактически невозможно, то мы не можем узнать и φ(n). Следовательно, мы не можем узнать d. Но у получателя есть значение d, следовательно, он знает р и q и может перейти к расшифровке сообщения: E d≡ (M e) d(mod n) ≡ М ed(mod n) ≡ M Nφ(n)+1(mod n), N € Ν. Теперь применим малую теорему Ферма. Если а = M N(a и n почти стопроцентно взаимно простые), то, применяя теорему, мы получаем: E d≡ Ма φ(n)(mod n) ≡ M (mod n) = M, поскольку М < n, как мы договорились в начале.

Из этого объяснения видно, что создать ключ расшифровки довольно легко, поскольку нужны всего два больших простых числа, р и q, а разложить его, напротив, очень трудно.

Bell, Е.Т., Los grandes matemdticos, Buenos Aires, Losada, 2010.

Boyer, C., Historia de la matematica, Madrid, Alianza Editorial, 2007.

Bradley, R., et Sandifer, E. (editores), Leonhard Euler: life, work and legacy, Amsterdam, Elsevier B.V., 2007.

Dunham, W., Euler, el maestro de todos nosotros, Madrid, Nivola,

2000.

Galindo, A. et al., La obra de Euler: tricentenario del nacimiento de Leonhard Euler (1707-1783), Madrid, Instituto de Espana, 2009.

Stewart, I., Historia de las matemdticos, Madrid, Critica, 2008.

Vargas, G., Calzada, G., Euler, el matemdtico, Madrid, El rompeca- bezas, 2011.

Ars conjectandi 125

Dioptricae 141

Institutiones calculi differentialis 8, 3, 103, 107

Institutiones calculi integralis 8, 13, 103, 107

Introductio in analysin infinitorum 8, 13, 28, 31, 34, 51, 103, 104, 106

Principes généraux du mouvement des fl uides 97

RSA 129

Solutio facilis problematum

quorundam geometricorum diffi cillimorum 91

Vollstàndige anleitung zur algebra 141

алгоритм 64, 120, 138

Апери постоянная 65

Араго, Франсуа 39, 103

барицентр 92

Берлинская академия наук 9, 13, 24, 72, 77, 78, 91, 114, 116

Бернулли

Даниил 24, 37-39, 60, 65, 141

Иоганн 9, 13, 18-24, 61

Николай 24, 84

Якоб 9, 18, 19, 20-24, 48-50, 55, 124

брахистохрона 20-22

Бугер, Пьер 22, 25

Бэббидж, Чарльз 64, 65

Вейерштрасс, Карл 41, 56

Венн, диаграммы 101

Вольтер 39, 75-78

Гаусс, Карл Фридрих 19, 29, 91, 101, 103, 105, 127, 131-133

Герои Александрийский 87

Гзель, Катерина 13, 38, 60, 117

гидродинамика 7, 19, 24, 98

Гольдбах, Кристиан 11, 13, 24, 28, 37-39, 44-46, 50, 62, 82-85, 95, 110, 117, 131

проблема 11, 13, 82-85

граф 67-69

Гюйгенс, Христиан 48, 49, 102

Д’Аламбер, Жан Батист Лерон 71, 77, 78, 90, 91, 99

Декарт 13, 18, 22, 71, 79, 103, 130, 133

Дидона, задача 87

Дидро, Дени 90, 115

диск Эйлера 11, 140

Диофант Александрийский 118, 119

Евклид 26, 57, 94, 103, 130, 132, 135

жидкость 39, 71, 73, 97, 98

зубчатое колесо 7, 116, 117

интеграл 8, 10, 41, 42, 57, 60, 62, 71, 89, 90, 103, 104, 118

инцентр 92, 94

исчисление

вариационное 11, 22, 73, 85, 89, 90, 93, 96, 103, 150