Joaquin Sandalinas - До предела чисел. Эйлер. Математический анализ.

lim n→∞(1 + 1/n) n= e.

Так Якоб Бернулли одновременно нашел е — хотя и не он дал постоянной это имя — и впервые в истории сделал открытие, применив неизвестное до того времени понятие предела. К сожалению, и в этот раз постоянная е осталась без надлежащего признания, поскольку Якоб не связал ее с логарифмами. Число е обрело свое первое имя в 1690 году, когда Лейбниц обозначил его буквой b в письме Гюйгенсу. С этого момента переменная начала существовать. Ей наконец дали имя, хотя и не окончательное. Открытие связи постоянной с логарифмами было вопросом времени, и этот медленный процесс завершился, как мы уже сказали, в 1731 году, в письме Эйлера Гольдбаху.

Якоб Бернулли занялся константой е не только с целью решить задачу о процентных ставках. На ее изучение ученого подвиг ребус, а точнее задача о теории вероятностей и шляпах. Пьер Ремон де Монмор (1678-1719) и Якоб Бернулли столкнулись со следующей загадкой: на бал съехалось N гостей. Они сдали свои шляпы лакею. Для них были приготовлены специальные коробки с этикетками, чтобы не перепугать владельцев. Но в последний момент лакей, назначенный ответственным за шляпы, заболел, и его заменили другим, который, не зная приглашенных, положил шляпы в коробки как придется. Проблема возникает, когда гости разъезжаются и лакей отдает им шляпы. Некоторые получат свои, другие — нет. Какова вероятность того, что произойдет полная катастрофа и ни одна шляпа не будет возвращена своему законному владельцу? Ответ таков:

Pn = 1 - 1/1! + 1/2! - 1/3! + ... + (-1) N/N!

Эта величина очень похожа на сумму с пределом е. Действительно, ее пределом является 1/е. Если же гостей очень много, то есть N — большое число, то

P N= 1/e = 36,79 %.

С этого момента, в частности в серии статей, написанных начиная с 1736 года, Эйлер официально называл ее постоянной. Он дал ей определение и связал предел Якоба Бернулли с логарифмами, которым он также дал современное определение. Эйлер принял е за основу натуральных логарифмов и таким образом обессмертил ее, вычислив первые 18 цифр — возможно, с помощью прямой суммы первых 20 членов ряда, который он же сам и обнаружил:

e = 1 + 1/1! + 1/2! + 1/3! + ...

Если это так, то этот подвиг Эйлера можно считать невероятным, почти невозможным. Тем не менее ученый часто выказывал сверхчеловеческие вычислительные способности, и многие склонны верить, что он прибег именно к этому методу.

О том, почему Эйлер выбрал именно букву е, высказывалось множество версий. Несмотря на самые распространенные из них, здесь нет связи со словом "экспонента" на немецком языке или с первой буквой его собственного имени. Есть предположение, что изначально ученый хотел обозначить постоянную через а, но она уже была занята другой величиной в его вычислениях. В любом случае, Эйлер так и не объяснил причины своего выбора.

Большая часть сведений о е содержится в его шедевре "Введение в анализ бесконечных", написанном в Берлине и изданном в 1748 году. В нем Эйлер окончательно установил, что логарифм и возведение в степень являются обратными друг другу операциями, то есть

у - а xтогда и только тогда, когда x-log ay.

Эта формула истинна для любого основания а, в том числе для а = е. Есть еще один аспект, который относится к области анализа и возведению в степень с основанием е, — функция ƒ(x) = еx совпадает со своей производной:

de х/dx = e x.

Постоянная е — трансцендентное число, то есть его нельзя получить, решая алгебраическое уравнение с рациональными коэффициентами. Для доказательства трансцендентности какого-либо числа в первую очередь надо проверить его на иррациональность (число называется иррациональным, когда его нельзя выразить в виде соотношения двух целых чисел). Это совсем не простая задача, и Эйлеру это не удалось. Тем не менее он подошел довольно близко к правильному решению, найдя следующую непрерывную дробь:

Получив доказательство того, что эта дробь бесконечна, он показал:

(е-1)/2

является иррациональным числом. Наконец, в 1873 году Шарль Эрмит (1822-1901) доказал трансцендентность числа е.

Помимо полученного Эйлером, часто встречаются и такие записи числа е в виде дроби:

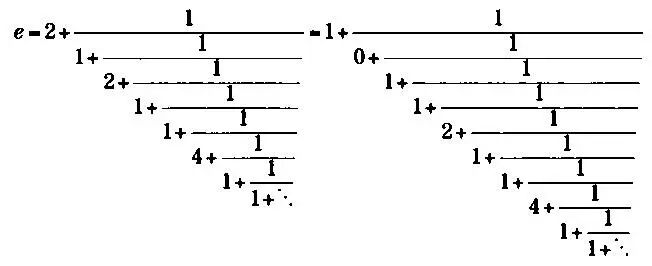
В последнее время в области теории чисел наблюдается возрастание интереса к вопросу о нормальности постоянных. Является ли е нормальным числом? В этом случае "нормальность" означает, что цифры в записи числа е сохраняют статистическое равновесие: если взять произвольное число, или пару чисел, или тройку и так далее, то вероятность того, что они появятся в записи числа е, всегда одна и та же.

То есть существуют нормальные и анормальные постоянные, но е кажется нормальным числом. Так или иначе, это всего лишь гипотеза, которую до сих пор никому не удалось доказать.

Арки колледжа святой Терезы (вверху) архитектора Антонио Гауди в Барселоне и Арка в Сент- Луисе (в середине) — примеры перевернутой традиционной цепной линии, образованной подвесными тросами (внизу). Формула этой линии содержит число е.

Существует математический вид спорта, который состоит в том, чтобы произнести наибольшее количество знаков после нуля какой-либо константы. Поскольку заучивать их, просто напрягая память, может быть скучно, для этого используются специальные фразы или стихи (mnemonics по-английски). Количество букв в каждом слове соответствует числовой последовательности, которую надо запомнить.

Например, название стихотворения "С десятью пушками по стороне" испанского поэта Хосе де Эспронседа можно соотнести с последовательностью 17727.

Это гораздо проще запомнить, чем само число, поскольку у слов есть смысл. Стало очень модно заучивать цифры числа к. Фразы для запоминания знаков числа е встречаются реже, но они тоже очень любопытны. В интернете можно найти такой вариант:

We present a mnemonic to memorize a constant so exciting that Euler exclaimed: '!' when first it was found, yes, loudly '!'. My students perhaps will compute e, use power or Taylor series, an easy summation formula, obvious, clear, elegant!