Ричард Фейнман - 9. Квантовая механика II

Фиг. 13.13. Сумма всех энергий электронов, ког­да нижние состояния на фиг. 13.8 заполнены n электронами (принято E 0=0).

Для первых двух электронов наклон функции постоянен — это прямая линия. Затем для каждой очередной группы электронов он воз­растает, меняясь скачком от одной группы к другой. Наклон изменяется тогда, когда заканчивается заполнение системы уровней с одной энергией и очередному электрону приходится переходить к очередной более высокой системе уровней.

В действительности истинная энергия иона бензола совер­шенно непохожа на фиг. 13.13 из-за взаимодействий электронов и из-за электростатических энергий, которыми мы пренебрегли. Эти поправки, однако, меняются с n довольно плавно. Даже если бы их все учесть, на окончательной энергетической кривой все равно остались бы изломы при таких и, при которых как раз заполняются отдельные уровни энергии.

Рассмотрим теперь очень гладкую кривую, на которой в среднем укладываются все точки (фиг. 13.14).

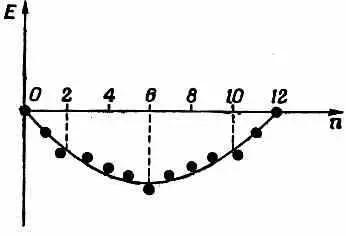
Фиг. 13.14. Точки с фиг. 13.13 и плавная кривая. Молекулы с n =2, 6, 10 устойчивее остальных.

Можно сказать, что точки над этой кривой обладают энергией «выше чем нор­мальной», а точки под нею «ниже чем нормальной». И в общем случае следует ожидать, что у конфигураций с «ниже чем нор­мальной» энергией средняя устойчивость окажется повышенной. Обратите внимание, что конфигурации, которые значительно ниже кривой, всегда оказываются в конце одного из прямоли­нейных отрезков, а именно там, где электронов как раз хватает на то, чтобы заполнить «энергетическую оболочку», как ее на­зывают. Это очень точное предсказание теории. Молекулы и ионы особо устойчивы (по сравнению с прочими подобными кон­фигурациями), когда имеющиеся у них в наличии электроны как раз заполняют энергетическую оболочку.

Эта теория объяснила и предсказала некоторые весьма нео­бычные химические факты. Вот очень простой пример. Возьмем кольцо из трех атомов. Почти невозможно поверить, что химик сможет из трех атомов составить кольцо и сделать его устой­чивым. Но это было сделано. Энергетический круг для трех электронов показан на фиг. 13.15.

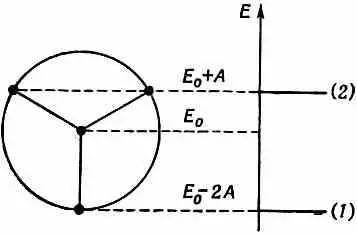
Фиг. 13.15. Энергетиче­ская диаграмма для кольца из трех атомов.

Если поместить в нижнее состояние два электрона, то пойдут в дело только два из трех требуемых электронов. Третий электрон придется поместить на более высокий уровень. Отсюда следует, что молекула не будет слишком устойчивой. Зато двухэлектронная структура обязана быть устойчивой. И действительно, оказывается, что нейтраль­ную молекулу трифенилциклопропанила сделать очень трудно, но зато сравнительно легко соорудить положительный ион, по­казанный на фиг. 13.16.

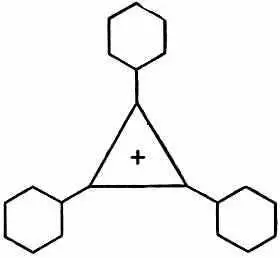
Фиг. 13.16. Катион трифенилииклопропанила.

Правда, кольцо из трех атомов никогда не бывает легко сделать, потому что, когда связи в органической молекуле образуют равносторонний треугольник, всегда появ­ляются большие напряжения. Чтобы соединение было устой­чиво, структуру нужно как-то стабилизировать. Оказывается, что, если поставить по углам три бензольных кольца, можно сделать положительный ион. (Отчего нужно добавлять бензоль­ные кольца, непонятно.)

Подобным же образом можно также проанализировать и пятиугольное кольцо. Если вы начертите энергетическую диа­грамму, то качественно сможете убедиться, что шестиэлектронная структура должна быть особо устойчива, так что такая мо­лекула должна быть устойчивее всего в виде отрицательного иона. И вот кольцо из пяти атомов действительно хорошо из­вестно, легко сооружается и действует всегда как отрицательный ион. Подобным же образом вы легко убедитесь, что кольцо из 4 и 8 атомов не очень интересно, а кольцо из 14 или 10 (как и кольцо из 6) должно быть особенно устойчиво в форме нейт­рального объекта.

§ 6. Другие применения приближения

Есть два других сходных случая, на которых мы остано­вимся лишь вкратце. Говоря о строении атома, можно считать, что электрон заполняет последовательные оболочки. Теорию движения электрона Шредингера удается с легкостью разра­ботать лишь для отдельного электрона, движущегося в «цент­ральном» поле — поле, зависящем только от расстояния от точки. Но как же тогда разобраться в том, что происходит в атоме, в котором 22 электрона?! Один из путей — воспользо­ваться приближением независимых частиц. Сперва вы подсчиты­ваете, что происходит с одним электроном. Получаете сколько-то там уровней энергии. Помещаете электрон в нижнее энерге­тическое состояние. В грубой модели вы продолжаете игнори­ровать взаимодействия электронов и продолжаете заполнять последовательные оболочки, но еще лучшие ответы получатся, если учесть (хотя бы приближенно) влияние электрического заряда электрона. Добавляя электрон, каждый раз вычис­ляйте амплитуду того, что он будет обнаружен в различных местах, и затем с ее помощью прикидывайте вид сферически симметричного распределения заряда. Поле этого распределе­ния (совместно с полем положительного ядра и всех предыдущих электронов) используйте для расчета состояний, доступ­ных очередному электрону. Таким путем вы можете получить вполне разумные оценки энергий нейтрального атома и раз­личных ионизованных состояний. Вы увидите, что и здесь имеются энергетические оболочки, так же как у электронов в кольцевой молекуле. При не совсем заполненной оболочке атом иногда охотнее присоединяет к себе один или несколько элект­ронов, а иногда охотнее их теряет, чтобы прийти в устойчивое состояние, когда оболочка заполнена.

Эта теория объясняет механизм, лежащий в основе самых фундаментальных химических свойств, проявляющихся в пе­риодической таблице элементов. Инертные газы — это те эле­менты, у которых как раз закончилось заполнение оболочки, и их особенно трудно заставить вступать в реакцию. (В действи­тельности, конечно, некоторые из них реагируют, например, с фтором или с кислородом, но в таких соединениях связь очень слаба; так называемые инертные газы инертны лишь отчасти.) Атом, у которого на один электрон больше или на один меньше, чем у инертного газа, легко теряет или присоединяет этот элект­рон, чтобы оказаться в особо устойчивых (низкоэнергетических) условиях, какие возникают от того, что оболочка заполнена до конца,— они являются очень активными химическими элемен­тами с валентностью +1 и -1.