Ричард Фейнман - 9. Квантовая механика II

Кроме того, в гл. 11 мы предположили, что амплитуды С(х n ) обязаны меняться во времени так, как положено по гамильтонову уравнению (11.3). В нашем новом обозначении это уравне­ние имеет вид

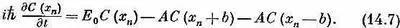
Два последних слагаемых в правой части представляют такой процесс, когда электрон, находившийся возле атома (n +1) или возле атома (n- 1), окажется возле атома ( n ).

Мы нашли, что (14.7) имеет решения, отвечающие состоя­ниям определенной энергии. Мы записывали их в виде

У состояний с низкой энергией длины волн велики (k мало) и энергия связана с k формулой

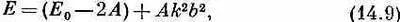
или, если выбрать нуль энергии так, чтобы было (Е 0 - 2 А)= 0, то энергия дается формулой (14.1).

Посмотрим, что бы произошло, если бы мы позволили рас­стоянию b между атомами решетки стремиться к нулю, сохра­няя волновое число постоянным. Если бы больше ничего не случилось, то последнее слагаемое в (14.9) обратилось бы просто в нуль, и никакой физики бы не осталось. Но предположим, что А и b вместе изменяются так, что при стремлении b к нулю произведение Ab 2 поддерживается постоянным: с помощью (14.2) мы запишем Аb 2 в виде постоянной h 2 /2m эфф . При этом (14.9) не изменится, но что произойдет с дифференциальным уравнением (14.7)?

Перепишем сперва (14.7) так:

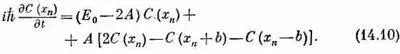
При нашем выборе Е 0первое слагаемое выпадет. Далее, пред­ставим себе непрерывную функцию С ( х ) , которая плавно про­ходит через значения С ( х n )в точках х n . Когда расстояние b стремится к нулю, точки х n сближаются все теснее и теснее и [если С ( х )меняется достаточно плавно] величина в скобках попросту пропорциональна второй производной С ( х ) . Можно написать (в чем легко убедиться, разложив в ряд Тэйлора каждый член) равенство

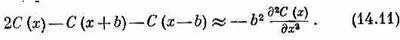
Тогда в пределе, когда b стремится к нулю, а b 2 A поддерживает­ся равным h2 /2m эфф , уравнение (14.7) переходит в

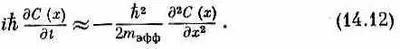
Перед нами уравнение, утверждающее, что скорость изменения С ( х ) — амплитуды того, что электрон будет обнаружен в х— зависит от амплитуды того, что электрон будет обнаружен в близлежащих точках так, что эта скорость пропорциональна второй производной амплитуды по координате.

Правильное квантовомеханическое уравнение движения электрона в пустом пространстве впервые было открыто Шре­дингером. При движении по прямой оно имеет вид (14.12); надо только m эффзаменить на m — массу электрона в пустом про­странстве. При движении по прямой в пустом пространстве уравнение Шредингера имеет вид

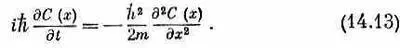
Мы не хотим, чтобы вы считали, будто мы сейчас вывели уравнение Шредингера; мы только показываем вам один из способов, каким его можно осмыслить. Когда Шредингер впер­вые написал его, он привел какой-то вывод, опиравшийся на эвристические доводы и блестящие интуитивные догадки. Не­которые из его доводов были даже неверны, но это не имело значения; важно то, что окончательное уравнение дает правиль­ное описание природы. И цель нашего обсуждения состоит просто в том, чтобы показать вам, что правильное фундаментальное квантовомеханическое уравнение (14.13) имеет ту же самую форму, какая получается в предельном случае электрона, дви­жущегося вдоль цепочки атомов. Это значит, что можно считать, что дифференциальное уравнение (14.13) описывает диффузию амплитуды вероятности от точки к точке вдоль прямой. Иначе говоря, если электрон имеет некоторую амплитуду того, что он будет в одной точке, то чуть позже у него появится амплитуда того, что он будет в близлежащих точках. Уравнение дейст­вительно напоминает уравнения диффузии, которыми мы поль­зовались в начале курса. Но есть и одно важное отличие: мни­мый коэффициент перед производной по времени приводит к по­ведению, в корне отличному от обычной диффузии (например, от диффузии газа, распространяющегося по длинной трубе). Обычная диффузия приводит к действительным экспоненциаль­ным решениям, а решения (14.13) суть комплексные волны.

§ 2. Волновая функция

Чтобы получить некоторое представление о том, как теперь все будет выглядеть, вернемся к самому началу и изучим проб­лему описания движения электрона по прямой, не рассматривая состояний, связанных с атомами решетки. Мы хотим возвратить­ся к самому началу и посмотреть, какими представлениями нужно пользоваться, чтобы описать движение свободной части­цы в пространстве. Раз нас интересует поведение частицы вдоль континуума точек, то придется иметь дело с бесконечным мно­жеством возможных состояний и, как вы увидите, идеи, которые были развиты для конечного числа состояний, потребуют неко­торых технических видоизменений.

Начнем с того, что вектором состояния | х >обозначим со­стояние, в котором частица расположена в точности в точке с координатой х. Для каждого значения х вдоль прямой — для 1,73, для 9,67, для 10,00 и т. д.— имеется соответствующее состояние. Выберем эти состояния | х >в качестве базисных. Если это сделать для всех точек х прямой, то получится полная совокупность состояний для движения в одном измерении. Теперь положим, что имеется состояние другого рода, скажем |y>, в котором электрон как-то распределен вдоль прямой. Один из способов описать это состояние — задать все амплиту­ды того, что электрон будет также найден в каждом из базисных состояний | x >. Надо задать бесконечную совокупность ампли­туд, по одной для каждого х. Запишем их в виде < x |y>. Каж­дая из этих амплитуд — комплексное число, и поскольку для каждого значения х существует одно такое число, амплитуда < x |y> является в действительности просто функцией х. Запи­шем ее также в виде С (х):