Ричард Фейнман - 9. Квантовая механика II

Теперь мы вернемся к обсуждению тех изменений в наших основных уравнениях, которые необходимо сделать для работы с континуумом базисных состояний. Когда имеется конечное число дискретных состояний, то фундаментальное условие, которому должна удовлетворять система базисных состояний, имеет вид

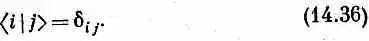
Если частица пребывает в одном базисном состоянии, то ампли­туда пребывания в другом базисном состоянии равна нулю. С помощью подходящей нормировки можно так определить амплитуду j >, чтобы она была равна единице. Оба эти условия содержатся в (14.36). Теперь мы хотим понять, как надо видоизменить это соотношение, когда пользуются базисными состояниями частицы на прямой. Если известно, что частица пребывает в одном из базисных состояний | х >, то какова ампли­туда того, что она пребывает в другом базисном состоянии |x'>? Если х и х' — две разные точки прямой, то амплитуда < x | х' >, конечно, есть нуль, что согласуется с (14.36). Но когда х и х' равны, то амплитуда < x | х' > не будет равна единице из-за той же старой проблемы нормировки. Чтобы увидеть, как надо все подправить, вернемся к (14.19) и применим это уравнение к частному случаю, когда состояние |j> — просто-напросто базисное состояние | х' > . Тогда получится

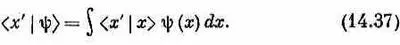
Далее, амплитуда — это как раз то, что мы назвали функцией y ( х ) . Подобно атому а амплитуда < x '|y>, по­скольку она относится к тому же состоянию y, является той же функцией переменной х', а именно y ( х' ) . Поэтому (14,37) можно переписать так;

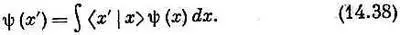
Уравнение должно выполняться для любого состояния y и, стало быть, для любой функции y ( х ) . Это требование обязано полностью определить природу амплитуды < x | х'), которая, конечно, есть попросту функция, зависящая от х и х'.

Наша задача теперь состоит в том, чтобы отыскать функцию f ( х, х' ) , которая после умножения на y ( х )и интегрирования по всем х даст как раз величину y ( х' ) . Но оказывается, что не существует математической функции, которая это умеет делать! По крайней мере не существует ничего похожего на то, что мы обычно имеем в виду под словом «функция».

Выберем какое-нибудь значение х', например 0, и опреде­лим амплитуду <0| x > как некую функцию х, скажем f ( х ) . Тогда (14.38) обратится в

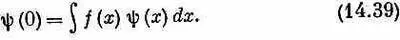
Какого же вида функция f ( х )могла бы удовлетворить такому уравнению? Раз интеграл не должен зависеть от того, какие значения принимает y ( х )при х, отличных от нуля, то ясно, что f ( х )должна быть равна нулю для всех значений х, кроме нуля. Но если f ( х )всюду равна нулю, то интеграл будет тоже равен нулю, и уравнение (14.39) не удастся удовлетворить. Возникает невозможная ситуация: нам нужно, чтобы функция была нулем всюду, кроме одной точки, и давала все же конечный интеграл. Что ж, раз мы не в состоянии сыскать функцию, которая так поступает, то простейший выход — просто сказать, что функция f(х) определяется уравнением (14.39). И именно f(х) — такая функция, которая делает (14.39) правильным. Функция, которая умеет это делать, впервые была изобретена Дираком и носит его имя. Мы обозначаем ее d ( х ) . Все, что о ней утверждается — это что функция d( х )обладает странным свойством: если ее подставить вместо f ( х )в (14.39), то интеграл выберет то значе­ние, которое y ( х )принимает при х= 0 ; и поскольку интеграл не должен зависеть от y ( х )при х, отличных от нуля, то функция d( х )должна быть нулем всюду, кроме х= 0 . Словом, мы пишем

<0| x >=d( x ), (14.40)

где d ( х )определяется соотношением

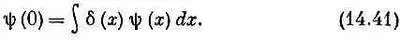
Посмотрите, что выйдет, если вместо y в (14.41) поставить частную функцию «1». Тогда получится

Иначе говоря, функция d( х )обладает тем свойством, что всюду, кроме х= 0 , она равна нулю, но интеграл от нее конечен и равен единице. Приходится вообразить, что функция d( х ) обладает в одной точке такой фантастической бесконечностью, что полная площадь оказывается равной единице.

Как представить себе, на что похожа d-функция Дирака? Один из способов — вообразить последовательность прямо­угольников (или другую, какую хотите функцию с пиком), которая становится все уже и уже и все выше и выше, сохраняя все время единичную площадь, как показано на фиг. 14.2.

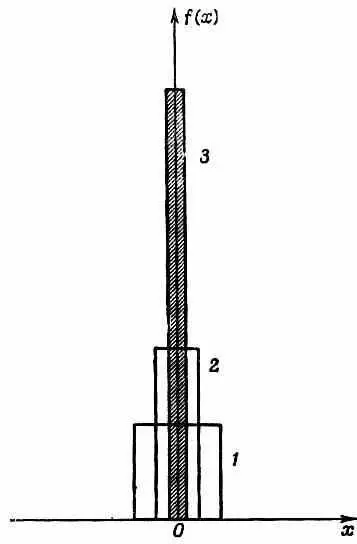
Фиг. 14.2. Последователь­ность функций, ограничиваю­щих единичную площадь, вид которых все сильнее и сильнее напоминает d-функцию.

Интеграл от этой функции от -Ґ до +Ґ всегда равен единице. Если вы умножите ее на произвольную функцию y( х )и проин­тегрируете произведение, то получите нечто, приближенно сов­падающее со значением функции при х= 0 , причем приближение становится все лучше и лучше, по мере того как прямоугольники становятся уже и уже. Если хотите, можете представлять d-функцию посредством такого рода предельного процесса. Но единственно здесь важно то, что d-функция определена так, что (14.41) справедливо для каждой волновой функции y ( х ) .

Это однозначно определяет d-функцию. Ее свойства тогда получаются такими, как было сказано.

Заменим аргумент d-функции с х на х- х', и соотношения обратят­ся в d( х-x ')=0,

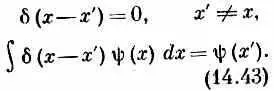
Если в (14.38) вместо амплитуды < x | х' > подставить d( x - х' ) , то это уравнение будет выполнено. В итоге получаем, что для наших базисных состояний с координатой х условие, соответствующее формуле (14.36), имеет вид

< x '| x >=d( x - х' ) . (14.44)

Теперь мы завершили все необходимые видоизменения наших основных уравнений, нужные для работы с континуумом ба­зисных состояний, соответствующих точкам на прямой. Обобще­ние на три измерения вполне очевидно: во-первых, координата х заменяется вектором r; во-вторых, интегралы по х заменяются на интегралы по х, у и z (иными словами, они становятся интегралами по объему); в-третьих, одномерную d-функцию надо заменить просто произведением трех d-функций от x , от y и от z : d ( х-х' ) d (у- у' ) d ( z-z' ). Собирая все вместе, получаем следующую совокупность уравнений для амплитуд частицы в трехмерном мире: