Ричард Фейнман - 9. Квантовая механика II

Мы не будем пытаться описывать другие последующие со­стояния. Подробное изложение волновых функций водорода вы найдете во многих книгах. Рекомендую вам особенно; L. Pauling, E.B.Wilson, Introduction to Quantum Mechanics, New York, 1935; R. B. Leightоn. Principles of Modern Physics, New York, 1959. В этих книгах вы найдете графики некоторых функций и графическое изображение многих со­стояний.

Хотелось бы упомянуть об одном особом свойстве волновых функций при высших l: при l >0 амплитуды обращаются в центре в нуль. Ничего в этом удивительного нет, ведь электрону трудно иметь большой момент, когда плечо момента очень мало. По этой причине чем l большe, тем дальше амплиту­ды «отталкиваются» от центра. Если вы посмот­рите, как радиальные функции F(r) меняются при малых r , то из (17.53) окажется, что

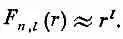
Такая зависимость от r означает, что при боль­ших l вам придется даль­ше отойти от r =0, чтобы получить заметную ампли­туду. Такое поведение, кстати, определяется чле­ном с центробежной силой в радиальном уравнении, так что все это применимо к любому потенциалу, который при малых r меняется медленнее, чем 1/r 2, а таково большинство атомных потенциалов.

§ 6. Периодическая таблица

Теперь мы хотели бы применить теорию атома водорода к объяснению химической периодической таблицы элементов. В атоме элемента с атомным номером Z имеется Z электронов, которые удерживаются электрическим притяжением ядра, но при этом взаимно отталкиваются друг от друга. Чтобы полу­чить точное решение, пришлось бы решить уравнение Шредин­гера для Z электронов в кулоновом поле. Для гелия уравнение имеет вид

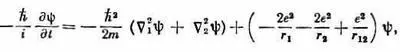
где С 2 1— лапласиан, который действует на r 1, координату пер­вого электрона; С 2 2действует на r 2, a r 12 =|r 1 - r 2|. (Мы опять пренебрегаем спинами электронов.) Чтобы найти стационар­ные состояния и уровни энергии, следовало бы отыскать ре­шения вида

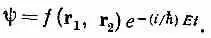
Геометрическая зависимость заключена в f — функции шести переменных — одновременных положений двух электронов. Аналитического решения никто не знает, хотя решения для низ­ших энергетических состояний и были найдены численными ме­тодами.

Когда электронов 3, 4 или 5, безнадежно пытаться получить точные решения. Поэтому было бы опрометчиво утверждать, что квантовая механика до конца объяснила периодическую таб­лицу. Но все же можно сказать, что даже с помощью довольно сомнительных приближений (и кое-какой последующей отделки) удается, по крайней мере качественно, понять многие хими­ческие свойства, проявляющиеся в периодической таблице.

Химические свойства атомов определяются в первую очередь их низшими энергетическими состояниями. Для отыскания этих состояний и их энергий мы воспользуемся следующей приближенной теорией. Во-первых, пренебрежем спином электрона, разве только что принцип запрета будет принят нами во вни­мание и мы будем считать, что каждое частное электронное состояние может быть занято только одним электроном. Это озна­чает, что на одной орбите не может оказаться больше двух электронов — один со спином, направленным вверх, другой — вниз. Затем мы в первом приближении пренебрежем деталями вза­имодействия электронов и будем считать, что каждый электрон движется в центральном поле, образуемом полями ядра и всех прочих электронов. Про неон, у которого 10 электронов, мы скажем, например, что каждый электрон в атоме неона испы­тывает влияние среднего потенциала ядра и оставшейся девятки электронов. Мы вообразим далее, что в уравнение Шредингера для каждого электрона мы подставляем V ( r ) — то же поле 1/ r , но только видоизмененное за счет сферически симметричной плотности заряда, возникшей от остальных электронов.

В такой модели каждый электрон ведет себя как независи­мая частица. Угловые зависимости его волновой функции бу­дут попросту такими же, какие были у атома водорода. Это будут те же s -состояния, р -состояния и т. п., и у них будут раз­личные значения т. Раз V ( r )больше не следует закону 1 /r, то радиальная часть волновых функций слегка перекраивается, но качественно останется прежней, так что по-прежнему будет существовать радиальное квантовое число п. Энергии состоя­ний тоже станут немного иными.

Н

Что же при таких представлениях у нас получится с водо­родом? У основного состояния водорода l=m= 0и n =1; мы говорим, что у него электронная конфигурация 1 s. Энергия равна -13,6 эв. Это значит, что для отрыва электрона от атома нужно 13,6 эв энергии. Ее называют «энергией ионизации», W 1 . Большая энергия ионизации означает, что оторвать элект­рон трудно, но водород может отнять электрон у другого атома, а потому он химически активен.

Не

Теперь обратимся к гелию. Оба электрона в гелии могут находиться в одном и том же нижнем состоянии (только у одного спин направлен вверх, у другого — вниз). В своем наинизшем состоянии электрон движется в поле с потенциалом, который при малых r походит на кулонов потенциал с Z=2, а при больших r — на кулонов потенциал с Z=1. В результате возникает «водородоподобное» 1 s -состояние с несколько более низкой энер­гией. Оба электрона занимают одни и те же 1s-состояния ( l =0, m =0). Наблюдаемая энергия ионизации (требуемая на отрыв одного электрона) равна 24,6 эв. Поскольку теперь «оболочка» 1 s заполнена (больше двух электронов в нее не втиснешь), то практически не возникает тенденции уводить у других атомов электроны. Гелий химически инертен.

Li

Ядро лития имеет заряд 3. Состояния электрона опять бу­дут водородоподобны, и тройка электронов займет три нижних уровня энергии. Два по­падут в состояния 1 s, a третий пойдет в состояние n =2. Но вот с l =0 или с l =1? В водороде у этих состояний энергия одна и та же, в других же атомах это не так, и вот по какой причине. Вспомним, что у 2 s -состояния есть неко­торая амплитуда того, что оно окажется вблизи ядра, а у 2 р такой амплитуды нет. Это означает, что 2 s -электрон как-то ощутит тройной электрический заряд ядра Li, а 2 р -электрон останется там, где поле выглядит как кулоново поле единичного заряда. Добавочное притя­жение понизит энергию 2 s -состояния по сравнению с энер­гией 2 р -состояния. Уровни энергии примерно окажутся такими, как показано на фиг. 17.8 (сравните с соответствующей диаграм­мой на фиг. 17.7 для водорода).