Ричард Фейнман - 9. Квантовая механика II
- Название:9. Квантовая механика II
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - 9. Квантовая механика II краткое содержание
9. Квантовая механика II - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
p/2) и равна нулю при q=90°. Возводя ее в квадрат, видим, что вероятность встретить электрон меняется с q так, как показано на фиг. 17.5, и не зависит от j.
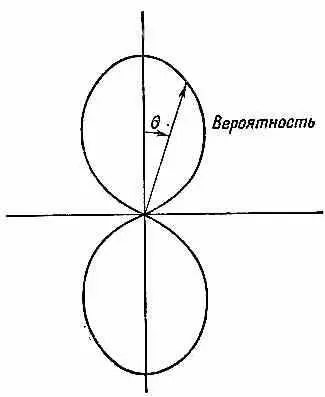
Фиг. 17.5. График cos 2q в полярных координатах, дающий относительную вероятность обнаружения электрона под различными углами к оси z (для данного r) в состоянии атома с l=1 и m =0.
Такое угловое распределение ответственно за то, что в молекулярной связи притяжение электрона в состоянии l= 1к другому атому зависит от направления. Отсюда ведет свое начало направленная валентность химического притяжения.
§ 4. Общее решение для водорода
В уравнении (17.35) мы записали волновые функции атома водорода в виде
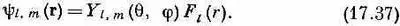
Эти волновые функции должны быть решениями дифференциального уравнения (17.7). Посмотрим, что это означает. Подставим (17.37) в (17.7); получим
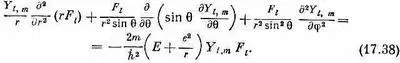
Помножим все на r 2 /F l и переставим члены; результат будет таков:
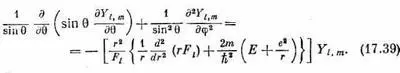
Левая часть этого уравнения зависит от q и j, а от r не зависит. Какое бы значение r мы ни взяли, от этого левая часть не изменится. Значит, то же должно быть выполнено и для правой части. Хотя в выражении в квадратных скобках там и сям попадаются разные r, все выражение от r зависеть не может, иначе бы не получилось уравнение, которое годится для всех r. Кроме того, как вы видите, эта скобка не зависит ни от q, ни от j. Она должна быть постоянным числом. Его величина имеет право зато зависеть от значения l того состояния, которое мы изучаем, поскольку этому состоянию принадлежит функция F l ; поэтому постоянное число мы обозначим K l . Уравнение (17.35), стало быть, равнозначно двум уравнениям
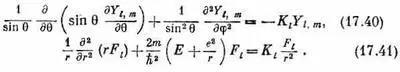
Теперь взглянем на то, что мы сделали. Для каждого состояния, описываемого числами l и m, мы знаем функции Y l , m ; тогда из уравнения (17.40) можно определить K l Затем, подставив K l в (17.41), мы получим дифференциальное уравнение для функции F l (r). Если мы его сможем решить, то все множители, входящие в (17.37), нам станут известны, и мы узнаем y(r).
Чему же равно К l ?Ну, во-первых, заметьте, что при всех т (входящих в данное l) оно должно быть одним и тем же, поэтому мы вправе выбрать в Y l , m то m, какое нам нравится, и вставить его в (17.40). Пожалуй, проще всего взять Y l,l . Из уравнения (16.24)
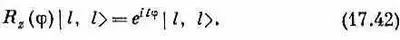
Матричный элемент R y (q) тоже совсем прост:
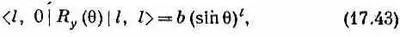
где b — некоторое число. Объединяя их, получаем

Подстановка этой функции в (17.40) даст

Теперь, когда мы определили К l , уравнение (17.41) даст нам радиальную функцию F l (r). Перед нами обычное уравнение Шредингера, у которого угловая часть заменена ее эквивалентом K l F l /r 2 . Перепишем (17.41) в той форме, в какой мы писали уравнение (17.8):
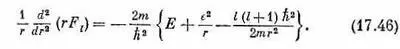
У потенциальной энергии появилась какая-то таинственная добавка. Хотя она появилась на свет после длинной серии математических шагов, тем не менее у нее простое физическое происхождение. Мы беремся рассказать о ее происхождении при помощи полуклассических аргументов. После этого она уже не покажется вам такой таинственной.
Представим классическую частицу, вращающуюся вокруг некоторого силового центра. Полная энергия сохраняется и является суммой потенциальной и кинетической энергий
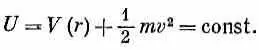
В общем случае v разлагается на радиальную компоненту v r и на касательную компоненту r q, т. е.
v 2 =v 2 r+ ( r q) 2.
Момент количества движения mr 2 qтоже сохраняется; пусть он равняется L. Тогда можно написать
mr 2q= L, или r q = L/mr ,
т. е. энергия равна
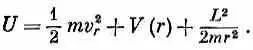
Если бы момента количества движения не было, у нас осталось бы только два первых члена. Добавление момента количества движения L изменяет энергию как раз так, как если бы к потенциальной энергии добавился член L 2 / 2 mr 2 . Но он почти точно совпадает с добавкой (17.46). Единственная разница в том, что вместо ожидаемого числителя l 2 h 2(этого можно было бы ожидать) появляется комбинация l ( l +1) h 2Но мы еще раньше видели [например, в гл. 34, § 7 (вып. 7)], что это обычная замена, к которой всегда приходится прибегать, если хотят, чтобы квазиклассические рассуждения совпали с правильным квантовомеханическим расчетом. Поэтому новый член можно понимать как своего рода «потенциал», определяющий «центробежную силу» и возникающий в уравнениях радиального движения вращающейся системы [см. гл. 12, § 5 (вып. 1)].
Теперь мы уже можем решить уравнение (17.46) относительно F l (r). Оно очень похоже на (17.8), так что прибегнем к той же технике. Все повторяется вплоть до уравнения (17.19), в котором появится добавочный член

Его можно записать еще и так:
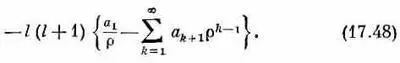
Интервал:
Закладка:






![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/1082376/pol-halpern-kvantovyj-labirint-kak-richard-fejnman.webp)

