Ричард Фейнман - 9. Квантовая механика II

Подстановка n =2 дает следующий более высокий уровень. В волновую функцию этого состояния входят два слагаемых. Она равна

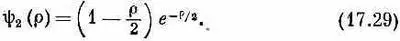
Волновая функция для следующего уровня равна

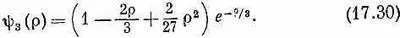
Эти три волновые функции начерчены на фиг. 17.2.

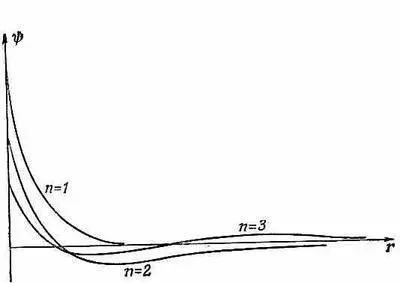
Фиг. 17.2. Волновые функции трех первых состоя­ний атома водорода с l =0. Масштабы выбраны так, чтобы полные вероятности совпадали.

Общая тен­денция уже видна. Все волновые функции при больших r, поко­лебавшись несколько раз, приближаются к нулю. И действи­тельно, число «изгибов» у y n как раз равно n, или, если угодно, число пересечений оси абсцисс — число нулей — равно n- 1.

§ 3. Состояния с угловой зависимостью

Мы нашли, что в состояниях, описываемых волновой функ­цией y n ( r ) , амплитуда вероятности обнаружить электрон сфе­рически симметрична; она зависит только от r — расстояния до протона. Момент количества движения таких состояний равен нулю. Теперь займемся состояниями, у которых какой-то момент количества движения имеется.

Можно было бы, конечно, просто исследовать чисто матема­тическую задачу отыскания функций от r, q и j, удовлетворяю­щих дифференциальному уравнению (17.7), добавив только физическое условие, что единственно приемлемые для нас функции — это такие, которые при больших r стремятся к нулю. Так почти всегда и поступают. Но мы попробуем несколько сократить наш путь и воспользоваться тем, что мы уже знаем, именно тем, что нам известно, как амплитуды зависят от про­странственных углов.

Атом водорода в том или ином состоянии — это частица с определенным «спином» j — квантовым числом полного мо­мента количества движения. Часть этого спина возникает от собственного спина электрона, другая — от движения электрона. Поскольку каждая из этих частей действует (в очень хорошем приближении) независимо, то мы по-прежнему будем игнориро­вать спиновую часть и учтем только «орбитальный» момент. Впрочем, это орбитальное движение в точности подобно спину. Скажем, если орбитальное квантовое число есть l, то z -компонента момента количества движения может быть l , l- 1, l -2, . . ., - l . (Мы, как обычно, измеряем все в единицах h .) Кроме того, по-прежнему годятся все наши матрицы поворота и прочие известные свойства. (Начиная с этого места, мы действительно начнем пренебрегать спином электрона; говоря о «мо­менте количества движения», мы будем иметь в виду только орбитальную его часть.)

Поскольку поле с потенциалом V, в котором движется элект­рон, зависит только от r, а не от q и не от j, то гамильтониан симметричен относительно поворотов. Отсюда следует, что и момент количества движения и все его проекции сохраняются. Это не есть особое свойство кулонова потенциала e 2 /r; оно спра­ведливо при движении в любом «центральном поле» — поле, зависящем только от r .

Представим себе некоторое возможное состояние электрона; внутренняя угловая структура этого состояния будет опреде­ляться квантовым числом l. В зависимости от «ориентации» полного момента количества движения относительно оси z его проекция т на ось z может равняться одному из 2 l +1 чисел между + l и - l. Пусть, например, m =1. С какой амплитудой электрон окажется на оси z на расстоянии r от начала? С нуле­вой. Электрон на оси z не может иметь какого-либо орбиталь­ного момента относительно этой оси. Но пусть тогда m =0. Вот это другое дело; теперь уже может появиться не равная нулю амплитуда того, что электрон окажется на оси z на таком-то расстоянии от протона. Обозначим эту амплитуду F l ( r ). Это — амплитуда того, что электрон будет обнаружен на расстоянии r по оси z, когда атом находится в состоянии | l, 0>, т. е. в состоянии с орбитальным моментом l и его z -компонентой m=0. А если нам известно F l ( r ), то известно все. Теперь уже в лю­бом состоянии | l, m >мы можем узнать амплитуду y lm ( r ) того, что электрон обнаружится в произвольном месте атома. Как мы это узнаем? А вот следите. Пусть у нас есть атом в состоянии | l, m > . Какова амплитуда того, что электрон обнару­жится под углом q, j и на расстоянии r от начала? Проведите новую ось z, скажем z', под этим углом (фиг. 17.3) и задайте вопрос: какова амплитуда того, что электрон окажется на новой оси z на расстоянии r ?

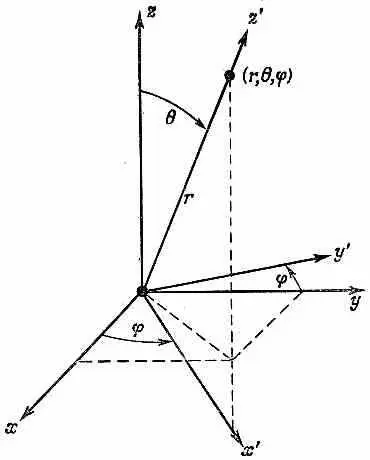
Фиг. 17.3. Точка (х, у, z) лежит на оси z' системы координат х' , у', z'.

Мы знаем, что он не сможет оказаться на оси z', если только m — его z'-компонента момента коли­чества движения — не равна нулю. Когда же m' =0, то амплитуда того, что электрон обнаружится на оси z', есть F l ( r ). Значит, результат получится перемножением двух амплитуд. Первая это амплитуда того, что атом, находящийся в состоянии | l, т > относительно оси z, окажется в состоянии | l, m'= 0> относи­тельно оси z' . Умножьте эту амплитуду на F l (r) и вы получите амплитуду y l , m( r) того, что электрон обнаружится в точке ( r , q, j) относительно первоначальной системы осей.

Давайте все это распишем. Матрицы преобразования для поворотов мы уже вычислили. Чтобы перейти от системы х, у, z к системе х', у', z' (см. фиг. 17.3), можно сперва сделать поворот вокруг оси z на угол j, а потом сделать поворот вокруг новой оси у (оси у') на угол q. Совместный поворот выразится произведением

R у (q) R z (j).

Амплитуда того, что после поворота обнаружится состояние | l , m' =0>, есть

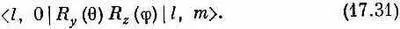
В итоге получаем

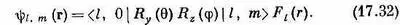
Орбитальное движение может обладать только целыми зна­чениями l. (Если электрон может быть обнаружен в любом месте, где r№ 0 , то имеется некоторая амплитуда того, что в этом на­правлении будет m =0. А состояния с m =0бывают только при целых спинах.) Матрицы поворота для l =1 приведены в табл.15.2 (стр. 129). Для больших l вы можете воспользоваться общими формулами, выведенными в гл. 16. Матрицы R z (j) и R y (q) написаны по отдельности, но как их комбинировать, вы знаете. В общем случае вы начнете с состояния | l , m > и подей­ствуете на него оператором R z (j), получив новое состояние R z (j)| l, т >(которое просто равно e im j | l, m > ) . Затем вы подействуете на это состояние оператором R y (q) и получите состояние R y (q) R z (j) | l , m >. Умножение на < l , 0| даст вам матричный элемент (17.31).