Ричард Фейнман - 9. Квантовая механика II

(Мы выделили первый член, а затем текущий индекс k сдвинули на единицу.) Вместо (17.20) появится

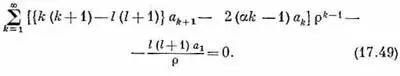
Поскольку член с r -1только один, то он должен обратиться в нуль. Коэффициент a 1должен быть равен нулю (если только l не равно нулю, но тогда мы приходим к нашему прежнему реше­нию). А когда все квадратные скобки при любых k обратятся в нуль, то и все следующие члены станут равны нулю. Из-за этого условие (17.21) переходит в

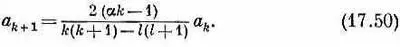
Это единственное существенное видоизменение по сравнению со сферически симметричным случаем.

Как и раньше, ряд должен оборваться, если мы хотим, чтобы решения представляли связанные электроны. Если a n =1, то ряд оборвется на k=n. Условие на а получается таким же: а должно быть равно 1/ n , где n — целое число. Однако (17.50) приводит и к новому ограничению. Индекс k не может быть равен l , в противном случае знаменатель обратится в нуль, а а l + 1— в бесконечность. Иначе говоря, поскольку a 1=0, то (17.50) подразумевает, что все последовательные a k обращаются в нуль, пока мы не придем к а l +1, которое может быть и не ну­лем. Это означает, что k должно начинаться с l +1 и кончаться

на п.

Окончательный итог таков: при любом l имеется набор возможных решений, которые мы обозначим F n , l , где n > l +1. Каждое решение обладает энергией

Волновая функция состояния с такой энергией и с угло­выми квантовыми числами l и m имеет вид

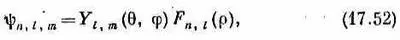
где

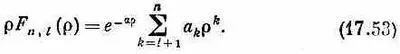
Коэффициенты a kполучаются из (17.50). Наконец-то в наших руках полное описание состояний атома водорода.

§ 5. Волновые функции водорода

Посмотрим же, что мы открыли. Состояния, которые удов­летворяют уравнению Шредингера для электрона в кулоновом поле, характеризуются тремя (причем целыми) квантовыми числами n, l, m. Угловое распределение амплитуды электрона может обладать только определенными формами, которые мы обозначим Y l , m . Они нумеруются числом l — квантовым числом полного момента количества движения я т — «магнитным» квантовым числом, которое может меняться от - l до + l . При каждой угловой конфигурации возможны различные радиаль­ные распределения F n , l (r) амплитуды электрона; они нумеруют­ся главным квантовым числом n, которое может меняться от l +1 до Ґ . Энергия состояния зависит только от n и растет с n. Состояние наинизшей энергии, или основное, является s -состоянием. У него l= 0 , n =1 и m= 0 . Это «невырожденное» состояние: имеется только одно состояние с такой энергией, а волновая функция у него сферически симметрична. Амплитуда того, что электрон обнаружится, достигает максимума в центре и монотонно спадает с удалением от центра. Эту электронную амплитуду можно изобразить этаким комочком (фиг. 17.6, а ).

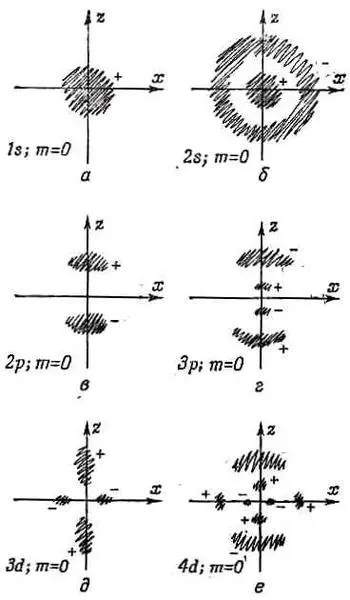
Фиг. 17.6. Наброски, отражающие общий харак­тер волновых функций водорода.

В заштрихованных местах ам­плитуды велики. Знаки плюс и минус — это относительные знаки амплитуд в каждой об­ласти.

Имеются и другие s-состояния, с большими энергиями; у них n =2, 3, 4, ... и l= 0 . Каждой энергии соответствует толь­ко одно состояние m= 0 , и все они сферически симметричны. Амплитуды этих состояний с ростом r один или несколько раз меняют знак. Имеется n- 1 сферических узловых поверхностей, или мест, где y проходит через нуль. Например, 2 s -состояние ( l =0, n= 2 ) выглядит так, как показано на фиг. 17.6, б. (Темные области указывают те места, где амплитуда велика, а знаки плюс и минус отмечают относительные фазы амплитуды.) Уровни энергии s-состояний показаны в первом столбце фиг. 17.7.

Фиг. 17.7. Диаграмма уров­ней энергии водорода.

Затем бывают р -состояния с l= 1 . Для каждого n (n равно или больше 2) существует тройка состояний с одинаковой энергией, одно с m =+1, другое с m =0, третье с m=- 1. Уровни энергии отмечены на фиг. 17.7. Угловые зависимости этих состояний приведены в табл. 17.1. Так, при m= 0 , если амплитуда положи­тельна для углов q, близких к нулю, то при углах q, близких к 180°, она окажется отрицательной. Имеется узловая плос­кость, совпадающая с плоскостью ху. При n >1 бывают также конические узловые по­верхности. Амплитуда n =2, m =0 намечена на фиг. 17.6, в, а волновая функция n =3, m= 0 — на фиг. 17.6, г.

Могло бы показать­ся, что поскольку т дает, так сказать, «ори­ентацию» в простран­стве, то должны наблю­даться еще такие же распределения, но с пи­ками вдоль оси х или вдоль оси у. Можно по­думать, что это скорее всего состояния с m =+1 и с m =-1. Однако это не так! Но зато раз у нас есть тройка состояний с одинаковыми энер­гиями, то любая линейная комбинация из этой тройки тоже будет стационарным состоянием с той же энергией. Оказы­вается, что « x »-состояние (по аналогии с « z »-состоянием, или состоянием с m =0, см. фиг. 17.6, в) это линейная комбинация состояний с m =+1' и с m =-1. Другая комбинация дает « y »-состояние. Точнее, имеется в виду, что состояния

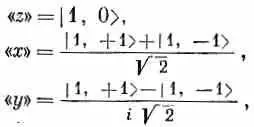
если отнести их к своим осям, выглядят одинаково.

У d-состояний ( l =2) для каждой энергии есть пять возмож­ных значений т; наинизшей энергией обладает n =3. Уровни показаны на фиг. 17.7. Угловые зависимости усложняются. К примеру, состояния с m =0 обладают двумя коническими узловыми поверхностями, так что при переходе от северного по­люса к южному волновая функция меняет фазы с + на — и обратно на +. Примерная форма амплитуды нарисована на фиг. 17.6, д и е для состояний с m =0 и n =3 и 4. И снова при больших n появляются конические узловые поверхности.