Ричард Фейнман - 9. Квантовая механика II

В этом примере J ^ z|y> — это умноженное на h/i e состояние, получаемое тоща, когда вы повернете |y> на малый угол e и затем вычтете прежнее состояние. Оно представляет «состоя­ние», являющееся разностью двух состояний.

Еще один пример. Мы имели оператор р^ х , он назывался опе­ратором ( x -компоненты) импульса и определялся уравнением, похожим на (18.6). Если D^ x ( L ) — оператор, который смещает состояние вдоль х на длину L, то р^ х определялось так:

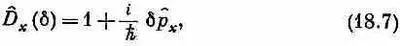
где d — малое смещение. Смещение состояния |y> вдоль оси х на небольшое расстояние d дает новое состояние |y'>. Мы го­ворим, что это новое состояние есть старое состояние плюс еще новый кусочек

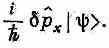
Операторы, о которых мы говорим сейчас, действуют на вектор состояния, скажем на |y>, являющийся абстрактным описанием физической ситуации. Это совсем не то, что алгебра­ические операторы, действующие на математические функции. Например, d/dx это «оператор», действие которого на f ( x )соз­дает из f ( x )новую функцию f' ( x ) =df/dx. Другой пример ал­гебраического оператора — это С 2. Можно понять, отчего в обоих случаях пользуются одним и тем же словом, но нужно помнить, что это разные типы операторов. Квантовомеханический оператор А действует не на алгебраическую функцию, а на вектор состояния, скажем на |y>. В квантовой механике употребляются и те и другие операторы, и часто, как вы уви­дите, в уравнениях сходного типа.

Когда вы впервые изучаете предмет, то все время надо иметь в виду эту разницу. А позднее, когда предмет вам станет ближе, вы увидите, что не так уж важно делать резкое различие между одними операторами и другими. И во многих книгах, как вы убедитесь, оба типа операторов обозначаются одинаково!

Теперь нам пора продвинуться вперед и узнать о мно­гих полезных вещах, которые можно проделывать с помощью операторов. Но для начала небольшое замечание. Пускай у нас имеется оператор А^, матрица которого в каком-то базисе есть A ij = | A^ | j >. Амплитуда того, что состояние A ^|y> находится также в некотором другом состоянии |j>, есть A ^|y>. Имеет ли смысл комплексное сопряжение этой амплитуды? Вы, вероятно, сможете показать, что

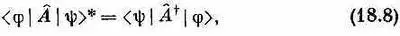
где А^ + (читается «А с крестом») это оператор, матричные эле­менты которого равны

A + ij =( A ji )*. (18.9)

Иначе говоря, чтобы получить i, j -и элемент матрицы А + , вы обращаетесь к j, i -му элементу матрицы А (индексы пере­ставлены) и комплексно его сопрягаете. Амплитуда того, что состояние А^ + |j> находится в состоянии |y>, комплексно сопряжена амплитуде того, что А^ |y> находится в |j>. Опера­тор А^ + называется «эрмитово сопряженным» оператору А^. Мно­гие важные операторы квантовой механики имеют специальное свойство: если вы их эрмитово сопрягаете, вы опять возвращае­тесь к тому же оператору. Если В как раз такой оператор, то В^ + =В^ ;его называют «самосопряженным», или «эрмитовым», оператором.

§ 2. Средние энергии

До сих пор мы в основном напоминали вам о том, что вы уже знаете. А теперь перейдем к новому. Как бы вы подсчитали среднюю энергию системы, скажем, атома? Если атом находится в определенном состоянии с определенной энергией и вы эту энергию измеряете, то вы получите определенную энергию Е. Если вы начнете повторять измерения с каждым из множества атомов, которые отобраны так, чтобы быть всем в одинаковом состоянии, то все измерения дадут вам Е, и «среднее» изо всех ваших измерений тоже, конечно, окажется Е.

Но что случится, если вы проделаете свои измерения над состоянием |y>, которое не является стационарным? Раз у си­стемы нет определенной энергии, то одно измерение даст одну энергию, то же измерение над другим атомом в том же состоя­нии даст другую и т. д. Каким же окажется среднее всей серии измерений энергии?

На этот вопрос мы ответим, если возьмем проекцию состоя­ния |y> на систему состояний с определенной энергией. Чтобы помнить, что это особый базис, будем обозначать эти состояния |h i >. Каждое из состояний |h i > обладает определенной энер­гией E i , В этом представлении

Когда вы проделываете измерение энергии и получаете некото­рое число Е i , вы тем самым обнаруживаете, что система была в состоянии |h i >. Но в каждом новом измерении вы можете получить новое число. Иногда вы получите E 1 , иногда Е 2 , иногда Е 3и т. д. Вероятность, что вы обнаружите энергию E 1?равна попросту вероятности обнаружить систему в состоянии |h 1>, т. е. квадрату модуля амплитуды С 1=1|y>. Вероятность обнаружить то или иное возможное значение энергии E i есть

P i = | C i | 2. (18.11)

Как же связать эти вероятности со средним значением всей последовательности измерений энергий? Вообразим, что мы получили ряд результатов измерений, например E 1 , Е 7 , E 11 , Е 9 , E 1, E 10 , Е 7 , E 2 , Е 3 , Е 9 , Е 6 , E 4и т. д., всего тысяча измерений. Сложим все энергии и разделим на 1000. Это и есть среднее. Можно сложение проделать и покороче. Посчитайте, сколько раз у вас вышло E 1(скажем, оно вышло N 1раз), сколько раз вышло Е 2(скажем, N 2раз) и т. д. Ясно, что сумма всех энер­гий равна

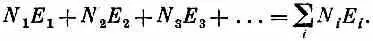
Средняя энергия равна этой сумме, деленной на полное число измерений, т. е. на сумму всех N i , которую мы обозначим N:

Мы почти у цели. Под вероятностью какого-нибудь собы­тия мы понимаем как раз число случаев, когда ожидается на­ступление этого события, деленное на общее число испытаний. Отношение N i /N должно (при больших N) мало отличаться от P i — вероятности обнаружить состояние |h i >, хоть и не будет точно совпадать с Р i из-за статистических флуктуации. Обозначим предсказываемую (или «ожидаемую») среднюю энер­гию < E > ср; тогда мы вправе сказать