Ричард Фейнман - 9. Квантовая механика II
- Название:9. Квантовая механика II
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - 9. Квантовая механика II краткое содержание
9. Квантовая механика II - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:

Те же рассуждения подойдут к измерениям каких угодно величин. Среднее значение измеряемой величины А должно равняться
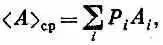
где a i — различные допустимые значения наблюдаемой величины, а Р i — вероятность получения этого значения.
Вернемся теперь к нашему квантовомеханическому состоянию |y>. Его средняя энергия равна
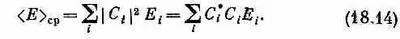
А теперь следите внимательно! Сначала перепишем эту сумму так:
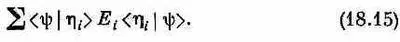
Теперь будем рассматривать левое
Вынесем его за знак суммы и напишем
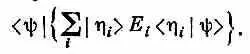
Это выражение имеет вид , где |j> — некоторое «придуманное» состояние, определяемое равенством
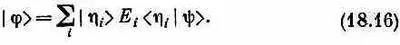
Иными словами, это то состояние, которое у вас получится, если вы возьмете каждое базисное состояние |h i > в количестве
Е i i |y>.
Но вспомним теперь, что такое |h i >. Состояния |h i > считаются стационарными, т. е. для каждого из них
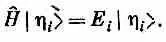
А раз Е i — просто число, то правая часть совпадает с |h i > Е i , а сумма в (18.16) — с
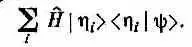
Теперь приходится просуммировать по i общеизвестную комбинацию, приводящую к единице:
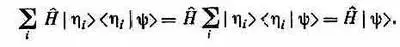
Чудесно, уравнение (18.16) совпало с

Средняя энергия состояния |y> записывается, стало быть, в очень привлекательном виде

Чтобы получить среднюю энергию, подействуйте на |y> оператором Н^ и затем умножьте на какую угодно совокупность базисных состояний, и, если мы знаем гамильтонову матрицу Н ij для этой совокупности, мы уже сможем узнать среднюю энергию. Уравнение (18.18) говорит, что при любой совокупности базисных состояний | i > средняя энергия может быть вычислена из
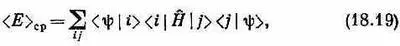
где амплитуды < i|H | j > как раз и есть элементы матрицы H ij . Проверим это на том частном примере, когда состояния | i > суть состояния с определенной энергией. Для них H ^| j >= e | j >, так что < i | H ^| j >= E j d ij и
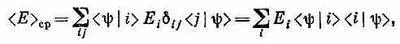
что вполне естественно.
Уравнение (18.19) можно, кстати, обобщить и на другие физические измерения, которые вы в состоянии выразить в виде оператора. Например, пусть L^ z есть оператор z -компоненты момента количества движения L. Средняя z -компонента для состояния |y> равна
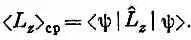
Один из способов доказательства этой формулы — придумать такую задачу, в которой энергия пропорциональна моменту количества движения. Тогда все рассуждения просто повторятся. Подытоживая, скажем, что если физически наблюдаемая величина А связана с соответствующим квантовомеханическим оператором А^, то среднее значение А в состоянии |y> дается формулой

Под этим подразумевается

где

§ 3. Средняя энергия атома
Пусть мы хотим узнать среднюю энергию атома в состоянии, описываемом волновой функцией y( r); как же ее найти? Рассмотрим сперва одномерную задачу, когда состояние |y> определяется амплитудой < x |y>=y ( x ). Нас интересует частный случай применения уравнения (18.19) к координатному представлению. Следуя нашей обычной процедуре, заменим состояния | i > и | j > на | х >и | х' >и сумму на интеграл. Мы получим
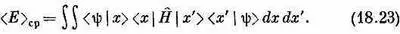
Этот интеграл можно при желании записывать иначе:
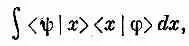
где
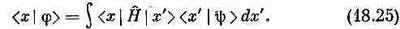
Интеграл по х' в (18.25) тот же самый, что встречался нам в гл. 14 [см. (14.50) и (14.52)]. Он равен
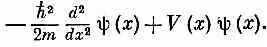
Поэтому можно написать
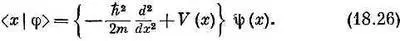
Вспомним, что x >=< x |y>*=y*( x ); с помощью этого равенства среднее значение энергии в (18.23) можно записать в виде
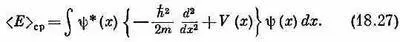
Если волновая функция y ( x ) известна, то, взяв этот интеграл, вы получите среднюю энергию. Вы теперь начинаете понимать, как от представлений о волновом векторе можно перейти к представлению о волновой функции и обратно.
Величина в фигурных скобках в (18.27) это алгебраический оператор. [«Оператор» V(x) означает «умножь на V ( x ) ». ]Мы обозначим его 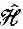
Интервал:
Закладка:






![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/1082376/pol-halpern-kvantovyj-labirint-kak-richard-fejnman.webp)

