Ричард Фейнман - 9. Квантовая механика II

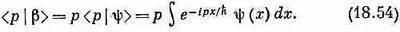
Интеграл берется по х, поэтому р можно внести под интеграл

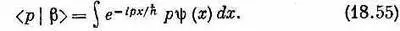
Теперь сравним это с (18.53). Может быть, вы подумали, что < x |b> равно p y( x )? Нет, напрасно! Волновая функция < х |b>=b( x ) может зависеть только от х, но не от р . В этом-то вся трудность.

К счастью, кто-то заметил, что интеграл в (18.55) мо­жно проинтегрировать по частям. Производная e - ipx / h по х равна (-i/h)pe - ipx / h , поэтому интеграл (18.55) это все равно, что

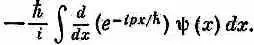
Если это проинтегрировать по частям, оно превратится в

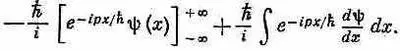
Пока речь идет только о связанных состояниях, y( x ) стремится к нулю при х® ±Ґ, скобка равна нулю и мы имеем

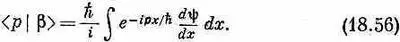
А вот теперь сравним этот результат с (18.53). Вы видите, что

Все необходимое, чтобы взять интеграл в (18.52), у нас уже есть. Окончательный ответ таков:

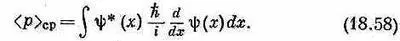
Мы узнали, как выглядит (18.48) в координатном представлении. Перед нами начинает постепенно вырисовываться интересная картина. Когда мы задали вопрос о средней энергии состояния |y>, то ответ был таков:

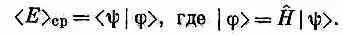
То же самое в координатном мире записывается так:

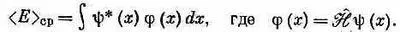
Здесь 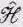— алгебраический оператор, который действует на функцию от х.

Когда мы задали вопрос о среднем значении х, то тоже обнаружили, что ответ имеет вид

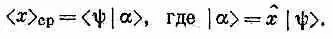
В координатном мире соответствующие уравнения таковы:

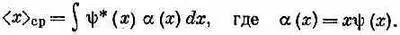
Когда мы задали вопрос о среднем значении р, то ответ оказался

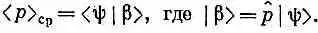
В координатном мире эквивалентные уравнения имели бы вид

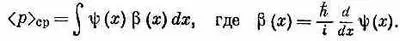
Во всех наших трех примерах мы исходили из состояния |y> и создавали новое (гипотетическое) состояние с помощью квантовомеханического оператора. В координатном представле­нии мы генерируем соответствующую волновую функцию, дей­ствуя на волновую функцию y ( x ) алгебраическим оператором. Можно говорить о взаимнооднозначном соответствии (для одно­мерных задач) между

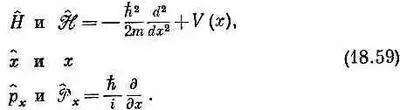
В этом перечне мы ввели новый символ 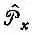для алгебраического оператора (h/i)д/дx:

и поставили под 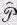значок х, чтобы напомнить, что имеем пока дело с одной только x -компонентой импульса.

Результат этот легко обобщается на три измерения. Для других компонент импульса

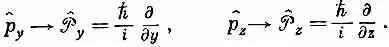
При желании можно даже говорить об операторе вектора импульса и писать

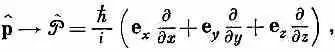
где е х , е y и е z — единичные векторы в трех направлениях. Можно записать это и еще изящнее:

Окончательный вывод наш таков: по крайней мере для некоторых квантовомеханических операторов существуют соот­ветствующие им алгебраические операторы в координатном пред­ставлении. Все, что мы до сих пор вывели (с учетом трехмер­ности мира), подытожено в табл. 18.1. Каждый оператор может быть представлен в двух равноценных видах:

либо

либо

Теперь мы дадим несколько иллюстраций применения этих идей. Для начала выявим связь между .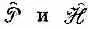

Если применить 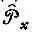дважды, получим

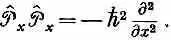
Это означает, что можно написать равенство

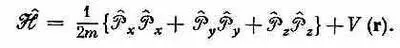
Или, в векторных обозначениях,

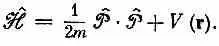
(Члены в алгебраическом операторе, над которыми нет символа оператора ^, означают простое умножение.) Это уравнение очень приятно, потому что его легко запомнить, если вы еще не забыли курса классической физики. Хорошо известно, что энергия (не­релятивистская) состоит из кинетической энергии р 2 /2m плюс потенциальная, а у нас 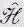— тоже оператор полной энергии. Этот результат произвел на некоторых деятелей столь силь­ное впечатление, что они начали стремиться во что бы то ни стало вбить студенту в голову всю классическую физику, прежде чем приступить к квантовой. (Мы думаем иначе!) Параллели очень часто обманчивы. Если у вас есть операторы, то важен порядок различных множителей, а в классическом уравнении он безраз­личен.