Ричард Фейнман - 9. Квантовая механика II

где

и смотрим, не удастся ли найти такой оператор х, чтобы он создавал состояние |a>, при котором уравнение (18.34) не противоречит уравнению (18.33). Иначе говоря, мы должны найти такое |a>, чтобы было

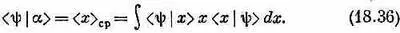
Разложим сперва по x -представлению:

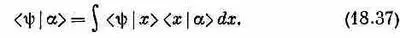
Сравним затем интегралы в (18.36) и (18.37). Вы видите, что в х-представлении (и только в этом представлении)

Воздействие на |y> оператора х^ для получения |a> равнознач­но умножению y ( x )=< x |y> на х для получения a ( х )=< x |a>. Перед нами определение оператора х^ в координатном представ­лении.

(Мы не задавались целью получить x -представление матрицы оператора х^. Если вы честолюбивы, попытайтесь показать, что

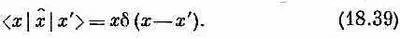
Тогда вы сможете доказать поразительную формулу

т. е. что оператор х^ обладает интересным свойством: когда он действует на базисное состояние | x >, то это равнозначно умножению на х. )

А может, вы хотите знать среднее значение x 2? Оно равно

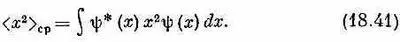
Или, если желаете, можно написать и так:

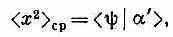
где

Под x ^ 2подразумевается х^х^ — два оператора применяются друг за другом. С помощью (18.42) можно подсчитать < x 2> ср, пользуясь каким угодно представлением (базисными состоя­ниями). Если вам нужно знать среднее значение х n или любого многочлена по х, то вы легко это теперь проделаете.

§ 5. Оператор импульса

Теперь мы хотим рассчитать средний импульс электрона, опять начав с одномерного случая. Пусть Р ( р ) dp — вероят­ность того, что измерение приведет к импульсу в интервале между р и p+dp. Тогда

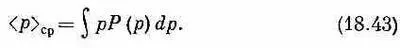
Обозначим теперь через < р |y> амплитуду того, что состоя­ние |y> есть состояние с определенным импульсом | р >. Это та же самая амплитуда, которую в гл. 14, § 3, мы обозначали <���имп. р |y>; она является функцией от р, как < x |y> является функцией от х. Затем мы выберем такую нормировку амплитуды, чтобы было

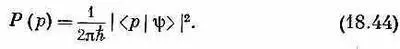
Тогда получится

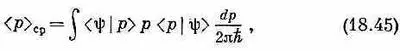
что очень похоже на то, что мы имели для < x > ср.

При желании можно продолжить ту же игру, которой мы предавались с < x > ср. Во-первых, этот интеграл можно записать так:

Теперь вы должны узнать в этом уравнении разложение амплитуды — разложение по базисным состояниям с определенным импульсом. Из (18.45) следует, что состояние |b> определяется в импульсном представлении уравнением

Иначе говоря, теперь можно писать

причем

где оператор р^ определяется на языке p -представления урав­нением (18.47).

[И опять при желании можно показать, что матричная запись р^ такова:

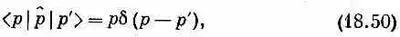
и что

Выводится это так же. как и для х.

Теперь возникает интересный вопрос. Мы можем написать < р > сртак, как мы это сделали в (18.45) и (18.48); смысл опе­ратора р^ в импульсном представлении нам тоже известен. Но как истолковать р^ в координатном представлении? Это бывает нужно знать, если у нас есть волновая функция y ( x )и мы со­бираемся вычислить ее средний импульс. Позвольте более четко пояснить, что имеется в виду. Если мы начнем с того, что за­дадим < p > cpуравнением (18.48), то это уравнение можно бу­дет разложить по p -представлению и вернуться к (18.45). Если нам задано p -представление состояния, а именно амплитуда < p |y> как алгебраическая функция импульса p , то из (18.47) можно получить < p |b> и продолжить вычисление интеграла. Вопрос теперь в следующем: а что делать, если нам задано описание состояния в x -представлении, а именно волновая функ­ция y ( x )=< x |y>?

Ну что ж, начнем раскладывать (18.48) в x -представлении.

Напишем

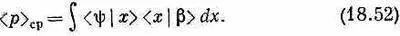
Но теперь надо знать другое: как выглядит состояние |b> в x -представлении. Если мы узнаем это, мы сможем взять ин­теграл. Итак, наша задача — найти функцию b ( x )=< x |b>. Ее можно найти следующим образом. Мы видели в гл. 14, § 3, как < р |b> связано с < x |b>. Согласно уравнению (14.24),

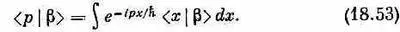
Если нам известно < р |b>, то, решив это уравнение, мы найдем < x |b>. Но результат, конечно, следовало бы как-то выразить через y ( x )=< x |y>, потому что считается, что именно эта ве­личина нам известна. Будем теперь исходить из (18.47) и, опять применив (14.24), напишем