Ричард Фейнман - 9. Квантовая механика II
- Название:9. Квантовая механика II
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - 9. Квантовая механика II краткое содержание
9. Квантовая механика II - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Таблица 18.1 · АЛГЕБРАИЧЕСКИЕ ОПЕРАТОРЫ В КООРДИНАТНОМ ПРЕДСТАВЛЕНИИ

В гл. 15 мы определили оператор р^ х через оператор смещения D^ x [см. формулу (15.27)]:
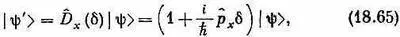
где d — малое смещение. Мы должны показать, что это эквивалентно нашему новому определению. В соответствии с тем, что мы только что доказали, это уравнение должно означать то же самое, что и
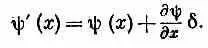
Но в правой части стоит просто разложение y (x+d ) в ряд Тэйлора, а y ( x +d)— то, что получится, если сместить состояние влево на б (или сдвинуть на столько же вправо систему координат). Оба наши определения р^ согласуются!
Воспользуемся этим, чтобы доказать еще кое-что. Пусть у нас в какой-то сложной системе имеется множество частиц, которым мы присвоим номера 1, 2, 3, ... . (Для простоты остановимся на одномерном случае.) Волновая функция, описывающая состояние, является функцией всех координат х 1 : х 2, x 3 ,... . Запишем ее в виде y (x 1, х 2 , х 3 , ...). Сдвинем теперь систему (влево) на d. Новая волновая функция
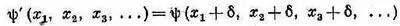
может быть записана так:
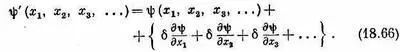
Согласно уравнению (18.65), оператор импульса состояния |y> (назовем его полным импульсом) равняется
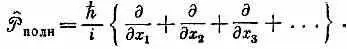
Но это все равно, что написать
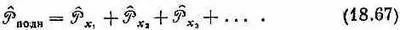
Операторы импульса подчиняются тому правилу, что полный импульс есть сумма импульсов отдельных частей. Здесь, как видите, все чудесным образом переплетено и разные вещи взаимно согласуются.
§ 6. Момент количества движения
Для интереса рассмотрим еще одну операцию — операцию орбитального момента количества движения. В гл. 15 мы определили оператор J^ z через R ^ z (j) — оператор поворота на угол j вокруг оси z. Рассмотрим сейчас систему, описываемую всего лишь одной-единственной волновой функцией y( r), которая является функцией одних только координат и не учитывает того факта, что спин у электрона должен быть направлен либо вверх, либо вниз. Это значит, что мы собираемся пока пренебречь внутренним моментом количества движения и намерены думать только об орбитальной части. Чтобы подчеркнуть различие, обозначим орбитальный оператор L^ z и определим его через оператор поворота на бесконечно малый угол e формулой
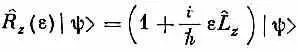
(напоминаем: это определение применимо только к состоянию |y>, у которого нет внутренних спиновых переменных, а есть только зависимость от координат r: х, у, z). Если мы взглянем на состояние |y> из новой системы координат, повернутой вокруг оси z на небольшой угол e, то увидим новое состояние:
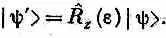
Если мы решили описывать состояние |y> в координатном представлении, т. е. с помощью его волновой функции y ( r), то следует ожидать такого равенства:

Что же такое 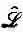 ? А вот что. Точка Р (х, у) в новой системе координат (на самом деле х', у', но мы убрали штрихи) раньше имела координаты x- ey и y +e x (фиг. 18.2).
? А вот что. Точка Р (х, у) в новой системе координат (на самом деле х', у', но мы убрали штрихи) раньше имела координаты x- ey и y +e x (фиг. 18.2).
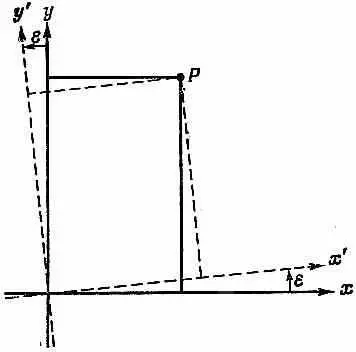
Фиг. 18.2. Поворот осей вокруг оси z на малый угол e .
Поскольку амплитуда того, что электрон окажется в точке Р , не меняется от поворота системы координат, то можно писать
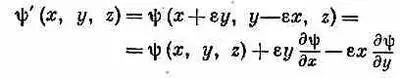
(напоминаем, что e — малый угол). Это означает, что
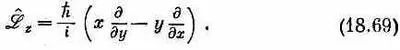
Это и есть наш ответ. Обратите, однако, внимание, что это определение эквивалентно такому:

Или, если вернуться к нашим квантовомеханическим операторам, можно написать

Эту формулу легко запомнить, потому что она похожа на знакомую формулу классической механики: это z-компонента векторного произведения
L= rX p.(18.72)
Одна из забавных сторон манипуляций с операторами заключается в том, что многие классические уравнения переносятся в квантовомеханическую форму. А какие нет? Ведь должны же быть такие, которые не получаются, потому что если бы все повторялось, то в квантовой механике не было бы ничего отличного от классической, не было бы новой физики.
Вот вам уравнение, которое отличается. В классической физике
хр х -р x х= 0 .
А что в квантовой механике?
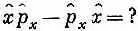
Подсчитаем это в x -представлении. Чтобы было видно, что мы делаем, приложим это к некоторой волновой функции y( x ) . Пишем
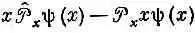
или
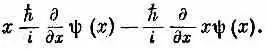
Вспомним теперь, что производные действуют на всё, что справа. Получаем
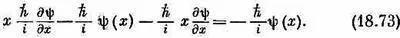
Интервал:
Закладка:






![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/1082376/pol-halpern-kvantovyj-labirint-kak-richard-fejnman.webp)

