Ричард Фейнман - 8a. Квантовая механика I

Это очень важный результат; перед нами общая теория поглощения света любой молекулярной или атомной системой. Хотя мы вначале считали, что состояние | I > обладает более высокой энергией, чем состояние | II >, но никакие наши рас­суждения от этого не зависели. Уравнение (7.55) соблюдается и тогда, когда энергия состояния | I > ниже энергии состояния | II >; тогда Р (I®II) представляет собой вероятность перехода с поглощением энергии от падающей электромагнитной волны. Поглощение атомной системой света всегда предполагает, что имеется амплитуда для перехода в колеблющемся электриче­ском поле между состояниями, отличающимися на энергию E = hw 0. В каждом отдельном случае она рассчитывается так же, как мы это проделали, и дает выражения наподобие (7.55). Поэтому мы подчеркнем следующие свойства этой формулы. Во-первых, вероятность пропорциональна Т. Иными словами, существует неизменная вероятность на единицу времени, что переход произойдет. Во-вторых, эта вероятность пропорцио­нальна интенсивности света, падающего на систему. В-третьих, вероятность перехода пропорциональна m 2, где, как вы помните, m x определяет энергетический сдвиг, вызываемый электриче­ским полем x. По этой именно причине m x появлялось и в урав­нениях (7.38) и (7.39) в качестве коэффициента связи, ответствен­ного за переход между стационарными состояниями | I > и | II >. Иными словами, для рассматривавшихся нами малых x член m x есть так называемое «возмущение» в матричном элементе гамильтониана, связывающем состояния |/> и |//>. В общем случае m x заменилось бы матричным элементом < II | H | I > (см. гл. 3, § 6).

В гл. 42, § 5 (вып. 4) мы говорили о связи между поглоще­нием света, вынужденным испусканием и самопроизвольным испусканием в терминах введенных Эйнштейном коэффициентов А и В. Здесь наконец-то в наших руках появляется квантовомеханическая процедура для подсчета этих коэффициентов. То, что мы обозначили Р ( I ® II ) для нашей аммиачной двухуровневой молекулы, в точности соответствует коэффициенту поглощения B nm в эйнштейновской теории излучения. Из-за сложности молекулы аммиака — слишком трудной для рас­чета — нам пришлось взять матричный элемент < II|H | I > в виде m x и говорить, что m извлекается из опыта. Для более про­стых атомных систем величину m mn , отвечающую к произвольному переходу, можно подсчитать, исходя из определения

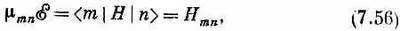
где Н mn — это матричный элемент гамильтониана, учитываю­щего влияние слабого электрического поля. Величина m mn , вычисленная таким способом, называется электрическим дипольным матричным элементом, Квантовомеханическая тео­рия поглощения и испускания света сводится тем самым к расчету этих матричных элементов для тех или иных атомных систем.

Итак, изучение простых систем с двумя состояниями (двух­уровневых) привело нас к пониманию общей проблемы поглощения и испускания света.

* Теперь мы опять будем писать | I> и | II> вместо |y I > и |y II >. Вы должны вспомнить, что настоящие состояния |y I > и |y II > суть энергетические базисные состояния, умноженные на соответствующий экспоненциальный множитель.

* Например, как легко убедиться, одно из допустимых решений имеет вид

* Очень жаль, но нам придется ввести новое обозначение. Раз бук­вы р и Е заняты у нас импульсом и энергией, то мы поостережемся опять обозначать ими дипольный момент и электрическое поле. Напомним, что в этом параграфе m означает электрический дипольный момент.

* В дальнейшем полезно (и читая, и произнося вслух) отличать арабские 1 и 2 и римские I и II. Мы считаем, что удобно для арабских, цифр резервировать названия «один» и «два», а I и II читать как «первый», «второй».

§ 1. Молекулярный ион водорода

§ 2. Ядерные силы

§ 3. Молекула водорода

§ 4.Молекула бензола

§ 5. Красители

§ 6.Гамильтониан частицы со спи­ном 1/2 в магнит­ном поле

§ 7.Вращающийся электрон в магнитном поле

§ 1. Молекулярный ион водорода

В предыдущей главе мы обсудили некото­рые свойства молекулы аммиака в предположении, что это система о двух состояниях (или двухуровневая система). На самом деле, конечно, это не так — у нее есть множество состояний: вращения, колебания, перемещения и т. д., но в каждом из этих состояний движе­ния следует говорить о паре внутренних со­стояний из-за того, что атом азота может быть переброшен с одной стороны плоскости трех атомов водорода на другую. Сейчас мы рас­смотрим другие примеры систем, которые в том или ином приближении можно будет считать системами с двумя состояниями. Многое здесь будет приближенным, потому что всегда име­ется множество других состояний, и в более точном анализе их следовало бы учитывать. Но в каждом из этих примеров мы окажемся в силах очень многое понять, рассуждая толь­ко о двух состояниях.

Раз мы будем иметь дело только с двух­уровневыми системами, то нужный нам га­мильтониан будет выглядеть так же, как и в предыдущей главе. Когда гамильтониан не зависит от времени, то известно, что имеются два стационарных состояния с определенными (и обычно разными) энергиями. В общем слу­чае, однако, мы будем начинать наш анализ с выбора базисных состояний (не обязательно этих стационарных состояний), таких, которые, скажем, имеют другой простой физический смысл. Тогда стационарные состояния систе­мы будут представлены линейной комбинацией этих базисных состояний.

Для удобства подытожим важнейшие уравнения, выведенные в гл. 7, Пусть первоначально в качестве базисных состояний были приняты | 1 > и | 2 > . Тогда любое состояние |y> пред­ставляется их линейной комбинацией:

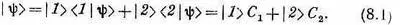
Амплитуды С i (под этим подразумеваются как C 1так и С 2) удовлетворяют двум линейным дифференциальным уравнениям