Ричард Фейнман - 8a. Квантовая механика I

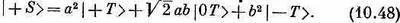
Точно так же легко показать, что

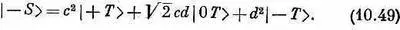
С |0 S > дело обстоит чуть посложнее, потому что

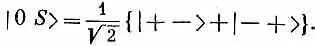
Но каждое из состояний | + - > и | - +> можно выразить через «штрихованные» состояния и подставить в сумму:

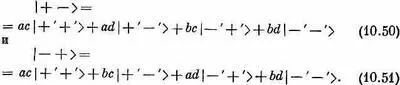
Умножая сумму (10.50) и (10.51) на 1/Ц2, получаем

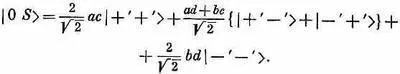
Отсюда следует

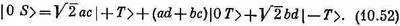
Теперь у нас есть все необходимые амплитуды. Коэффи­циенты в (10.48), (10.49) и (10.52) —это матричные элементы

< jТ | iS > . Сведем их в одну матрицу:

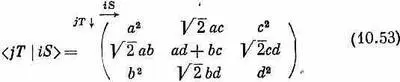
Мы выразили преобразование спина 1 через амплитуды а, b, с и d преобразования спина 1/ 2.

Если, например, система Т повернута по отношению к S на угол а вокруг оси у (см. фиг. 3.6, стр. 64), то амплитуды в табл. 10.4—это просто матричные элементы R y (a) в табл. 4.2:

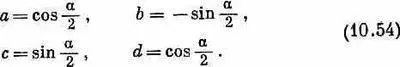
Подставив их в (10.53), получим формулы (3.38), которые приведены на стр. 80 без доказательства.

Но что же случилось с состоянием | IV )?! Это система со спи­ном нуль; значит, у нее есть только одно состояние — оно во всех системах координат одно и то же. Можно проверить, что все так и выходит, если взять разность (10.50) и (10.51); получим

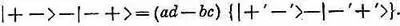
Но (ad-bc) — это определитель матрицы для спина 1/ 2, он просто равен единице. Получается

| IV '>=| IV > при любой относительной ориентации двух систем координат.

* Тем, кто перескочил через гл. 4, придется пропустить и этот па­раграф.

* Вспомните, что классически U= -m·B, так что энергия наименьшая, когда момент направлен по полю. Для положительно за­ряженных частиц магнитный момент параллелен спину, для отрицатель­ных — наоборот. Значит, в (10.27) m р — число положительное, а (m е — отрицательное.

*Crampton, Kleppner, Ramsey, Physical Review Letters, 11, 338 (1963).

*В действительности состоянием является

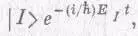
но, как обычно, мы отождествим состояния с постоянными векторами, которые при t=0 совпадают с настоящими векторами.

* Этот оператор сейчас называют оператор обмена спинами.

* Для этих операторов, правда, оказывается, что от их порядка ни­чего не зависит.