Ричард Фейнман - 8a. Квантовая механика I
- Название:8a. Квантовая механика I
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - 8a. Квантовая механика I краткое содержание
8a. Квантовая механика I - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Взяв гамильтониан (10.5), можно подставить его в уравнение

и посмотреть, что делает спиновое взаимодействие с уровнями энергии. Для этого надо подсчитать шестнадцать матричных элементов H ij = < i | H|j >, отвечающих любой двойке из четырех базисных состояний (10.1).
Начнем с того, что подсчитаем, чему равно Н^ |j > для каждого из четырех базисных состояний. К примеру,
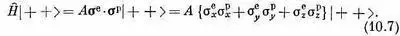
Пользуясь способом, описанным немного раньше (вспомните табл. 10.1, она очень облегчит дело), мы найдем, что каждая пара а делает с |+ +>· Ответ таков:

Значит, (10.7) превращается в
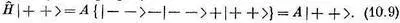
Таблица 10.2 · спиновые операторы ДЛЯ АТОМА ВОДОРОДА
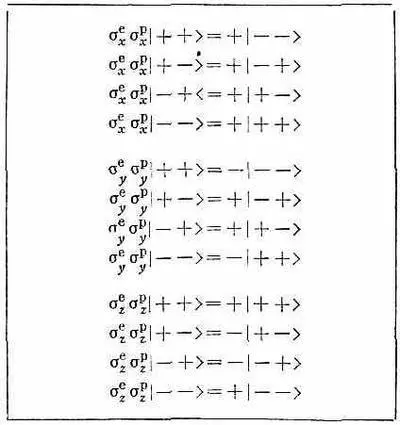
А раз все наши четыре базисных состояния ортогональны, то это немедленно приводит к
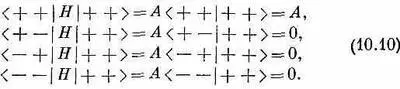
Вспоминая, что Н | i > =<.i | H | j >*, мы сразу сможем написать дифференциальное уравнение для амплитуды С 1:
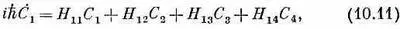
или
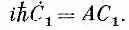
Вот и все! Только один член.
Чтобы теперь получить оставшиеся уравнения Гамильтона, мы должны терпеливо пройти через те же процедуры с H^, действующим на другие состояния. Во-первых, попрактикуйтесь в проверке того, что все произведения сигм в табл. 10.2 написаны правильно. Затем с их помощью получите

И тогда, умножая их все по порядку слева на все прочие векторы состояний, мы получаем следующую гамильтонову матрицу H ij :
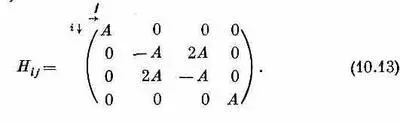
Это, конечно, означает, что дифференциальные уравнения для четырех амплитуд С i имеют вид
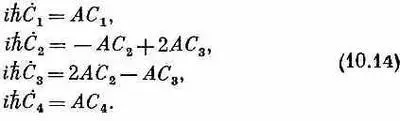
Но прежде чем перейти к их решению, трудно удержаться от того, чтобы не рассказать вам об одном умном правиле, которое вывел Дирак. Оно поможет вам ощутить, как много вы уже знаете, хотя нам в нашей работе оно и не понадобится. Из уравнений (10.9) и (10.12) мы имеем
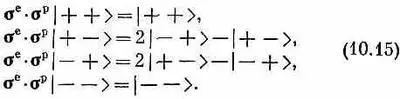
«Взгляните, — сказал Дирак, — первое и последнее уравнения я могу записать также в виде
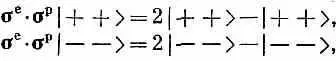
и тогда все они станут похожими. Теперь я придумаю новый оператор, который обозначу Р спин. обмени который, по определению, будет обладать следующими свойствами:

Оператор этот, как видите, только обменивает направления спина у двух частиц. Тогда всю систему уравнений (10.15) я могу написать как одно простое операторное уравнение:
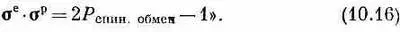
Это и есть формула Дирака. Оператор обмена спинами дает удобное правило для запоминания s е ·s p . (Как видите, вы теперь уже все умеете делать. Для вас все двери открыты.)
§ 3. Уровни энергии
Теперь мы готовы к тому, чтобы вычислить уровни энергии основного состояния водорода, решая гамильтоновы уравнения (10.14). Мы хотим найти энергии стационарных состояний. Это значит, что мы должны отыскать те особые состояния |y>, для которых каждая из принадлежащих |y> амплитуд C i =< i |y> обладает одной и той же зависимостью от времени, а именно е - w t . Тогда состояние будет обладать энергией E=hw . Значит, мы ищем совокупность амплитуд, для которых

где четверка коэффициентов а i не зависит от времени. Чтобы увидеть, можем ли мы получить эти амплитуды, подставим (10.17) в (10.14) и посмотрим, что из этого выйдет. Каждое ihdC i /dt в (10.14) перейдет в EC i . И после сокращения на общий экспоненциальный множитель каждое С i превратится в а i ; получим
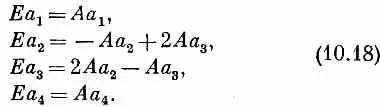
Это и нужно решить для отыскания a 1, а 2, а 3и а 4. Право, очень мило со стороны первого уравнения, что оно не зависит от остальных,— а это значит, что одно решение сразу видно. Если выбрать Е=А, то
a 1=1, a 2= a 3= a 4=0
даст решение. (Конечно, если принять все а равными нулю, то это тоже будет решение, но состояния оно не даст!) Будем считать наше первое решение состоянием | I >:
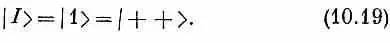
Его энергия
Е I =А.
Все это немедленно дает ключ ко второму решению, получаемому из последнего уравнения в (10.18):
а 1= а 2= а 3=0, а 4=1, Е=А.
Это решение мы назовем состоянием | II >:
|//> = |4> = |-->,(10.20)
Е II =А.
Дальше пойдет чуть труднее; оставшиеся два уравнения (10.18) переплетены одно с другим. Но мы все это уже делали. Сложив их, получим
Е(а 2 + а 3 ) = А(а 2 + а 3 ). (10.21)
Вычитая, будем иметь
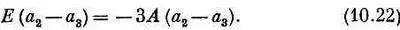
Интервал:
Закладка:






![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/1082376/pol-halpern-kvantovyj-labirint-kak-richard-fejnman.webp)

