Ричард Фейнман - 8. Квантовая механика I

где R ji — то же самое, что и < jT | iS > . Каждая амплитуда C j есть сумма по всем i одного ряда коэффициентов R ji , умно­женных на каждую амплитуду С i . Это выглядит так же, как преобразование вектора от одной системы координат к другой.

Но не будем слишком долго увлекаться абстракцией. Мы уже приводили парочку примеров этих коэффициентов для случая спина 1, и вы сами можете разобраться, как ими пользоваться практически. Но, с другой стороны, у квантовой механики существует очень красивое качество: из того факта, что состоя­ний только три, используя лишь свойства симметрии простран­ства относительно вращений она умеет чисто отвлеченным пу­тем вычислить эти коэффициенты. Приводить на столь ранней стадии эти рассуждения было бы нехорошо: прежде чем вы «вер­нулись бы на землю», вы могли бы утонуть в новом море абстрак­ций. Однако все это так красиво, что мы в свое время это не­пременно проделаем.

В этой же главе мы покажем вам, как можно получить коэффициенты преобразований для частиц со спином 1/ 2. Мы выбрали этот случай потому, что он проще спина 1. Задача состоит в том, чтобы определить коэффициенты R ji для частицы, или атомной системы, которая в аппарате Штерна — Герлаха расщепляется на два пучка„ Мы собираемся вывести все коэф­фициенты для преобразования от одного представления к дру­гому путем чистого рассуждения плюс несколько предположе­ний. Какие-то предположения всегда нужны для того, чтобы пользоваться «чистыми» рассуждениями! Хотя наши доказа­тельства будут абстрактными и немного запутанными, резуль­тат, который мы получим, сформулировать легко и понять просто; сам же по себе он будет очень важным. Можете, если угодно, рассматривать это как своего рода культмероприятие. Мы ведь условились уже, что все существенное, выведенное здесь, будет также выводиться по мере надобности в следующих главах другим путем. Так что вы не бойтесь потерять нить нашего изложения квантовой механики, если полностью про­пустите эту главу или изучите ее попозже. Мероприятие «куль­турное» в том смысле, что оно должно показать вам, что прин­ципы квантовой механики не только любопытны, но и настолько глубоки, что, прибавив к ним всего несколько добавочных ги­потез о структуре пространства, мы сможем вывести огромное множество свойств физических систем. Кроме того, важно по­нимать, откуда вытекают различные следствия квантовой ме­ханики. Пока наши законы физики неполны (а так оно и есть на самом деле), всегда интересно выяснить, в каких местах наши теории перестают согласовываться с опытом — там ли, где наша логика самая лучшая, или же там, где она наихудшая. До сих пор оказывалось, что там, где наша логика наиболее абстрактна, там она всегда дает правильные результаты — теория согласуется с опытом. Только тогда, когда мы пытаемся строить конкретные модели внутреннего устройства элементар­ных частиц и их взаимодействий, только тогда мы оказываемся не в состоянии найти теорию, согласную с экспериментом. Та теория, которую мы намерены описать здесь, согласуется с опытом всюду, где ее испытывали; она так же хороша для странных частиц, как и для электронов, протонов и т. д.

Еще одно неприятное (но важное) замечание: коэффициенты R jiневозможно определить однозначно, потому что в амплиту­дах вероятностей всегда есть какой-то произвол. Если у вас есть ряд каких угодно амплитуд, скажем амплитуд прихода в некоторое место по целому множеству различных путей, и если вы помножите каждую отдельную амплитуду на один и тот же фазовый множитель, скажем на е i d, то получится другая сово­купность, которая будет ничуть не хуже первой. Значит, всегда можно произвольно изменить фазу всех амплитуд в любой за­даче, если вы этого захотите.

Допустим, вы вычисляете некоторую вероятность, беря сумму нескольких амплитуд, скажем (А + В + С +...), и возводя ее модуль в квадрат. Затем кто-то другой вычисляет то же самое, складывая амплитуды (А' + В' + С'+ ...) и возводя их модуль в квадрат. Если все А', В', С' и т. д. отли­чаются от А, В, С и т. д. только множителем е i d, то все вероят­ности, получаемые возведением модуля в квадрат, окажутся в точности одинаковыми, потому что тогда (А' + В' + С +...) равно e i d (А + В + С+ ...). Или допустим, к примеру, что мы считали что-нибудь по уравнению (4.1), но затем внезап­но изменили все фазы определенной базисной системы. Каждую из амплитуд < i |y> тогда пришлось бы умножить на один и тот же множитель е i d . Точно так же изменились бы в e i d раз и все амплитуды: , но амплитуды i > комплексно сопряжены амплитудам < i |c>; тем самым они приобрели бы множитель е - i d . Плюс и минус id в экспонентах уничтожатся, и получится то же выражение, что было и раньше. Стало быть, общее правило таково, что изменение на одну и ту же фазу всех амплитуд по отношению к данной базисной системе или даже простое изменение всех амплитуд в любой задаче на одну и ту же фазу ничего не меняет. Значит, существует некоторая свобода в выборе фаз нашей матрицы преобразования. Мы то и дело будем прибегать к такому произвольному выбору, всегда сле­дуя общепринятым соглашениям.

§ 2. Преобразование к повернутой системе координат

Рассмотрим опять «усовершенствованный» прибор Штерна— Герлаха, описанный в предыдущей главе. Пучок частиц со спи­ном 1/ 2, входящих слева, расщепляется, вообще говоря, на два пучка, как показано схематически на фиг. 4.1.

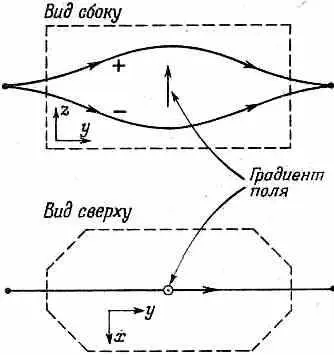
Фиг. 4.1. «Усовершенствованный» прибор Штерна — Герлаха с пучками частиц со спином 1/ 2.

(При спине 1 пучков было три.) Как и раньше, пучки в конце снова сводятся в одно место, если только один из них не будет перекрыт «перегородкой», которая перехватит его на полпути. На рисунке имеется стрелка, которая показывает направление роста величины поля, скажем положение магнитного полюса с острым наконечником. Эта стрелка пусть будет представлять собой на правление вверх для данного прибора. В каждом аппарате ее положение фиксировано, что позволяет указывать взаимную ориентацию нескольких приборов относительно друг друга. Наконец, предположим еще, что направление магнитного поля относительно стрелки во всех магнитах одинаково.

Будем говорить, что атомы из «верхнего» пучка находятся по отношению к этому прибору в состоянии (+), атомы из «нижнeгo» — в состоянии (-). (Нуль-состояния для спина 1/ 2не