Ричард Фейнман - 8. Квантовая механика I

существует.)

Положим теперь, что мы поставили два наших усовершен­ствованных прибора Штерна — Герлаха один за другим фиг. 4.2, а).

Фиг. 4.2. Два эквивалентных эксперимента.

Первый (назовем его S ) можно употребить на то, что­бы приготовлять чистое состояние (+ S ) или (- S ), загораживая то один, то другой пучок. [На рисунке приготовляется чистое состояние (+ S ).] При любом расположении всегда есть неко­торая амплитуда того, что частица, выходящая из S, окажется в пучке (+Т) или (- Т) второго прибора. Всего таких ампли­туд четыре: амплитуды перехода от (+ S ) к (+ T ), от (+S) к (-Т), от (-S) к (+Т) и от (- S ) к (- T ). Эти амплитуды — просто четыре коэффициента матрицы преобразования R jiперехода от представления S к представлению Т. Можно счи­тать, что первый прибор «приготовляет» определенное состояние в одном представлении, а второй «анализирует» это состояние в терминах второго представления. Мы хотим научиться отве­чать на такие вопросы: если, загородив один из пучков в S, мы приготовили атом в данном состоянии, например в состоянии (+5), то каково будет изменение, которое он испытает, пройдя через прибор Т, который настроен на состояние (- T )? Резуль­тат, конечно, будет зависеть от углов между системами S и Т.

Мы должны объяснить, почему есть надежда найти коэф­фициенты R ji теоретически. Почти невозможно поверить, что если у частиц спин был выстроен в направлении +z, то есть хоть какой-то шанс обнаружить, что ее спин ориентирован в направлении + x или в каком-либо другом направлении. Это дей­ствительно почти невозможно. Но все же не совсем. Это на­столько невозможно, что остается лишь один путь, каким это происходит, а если этот путь один, то его уже можно найти.

Первое рассуждение можно провести так. Предположим, что, как показано на фиг. 4.2, а, прибор Т направлен вверх под уг­лом а относительно S. Пусть через S проходит только пучок (+), а через Т — только пучок (-). Мы измерили некоторую вероятность того, что частицы, выходя из S, пройдут сквозь Т. Теперь предположим, что мы делаем второе измерение при­бором, показанным на фиг. 4.2, б. Относительная ориентация S и Т одинакова, но вся система расположена в пространстве под другим углом. Мы хотим предположить, что оба опыта приведут к одному и тому же значению вероятности того, что частица в чистом состоянии относительно S окажется в некото­ром определенном состоянии относительно Т, Иными словами, мы предполагаем, что результат любого опыта такого рода оди­наков, что сама физика одинакова, как бы весь прибор ни был ориентирован в пространстве. (Вы скажете: «Это самоочевидно». Но это все же только предположение, и оно «правильно» только тогда, если так действительно бывает.) Это означает, что коэффициенты R ji зависят лишь от взаимного расположения S и Т в пространстве, а не от абсолютного их расположения. Выражаясь иначе, R ji зависит только от поворота, который переводит S в Т, потому что общим для фиг. 4.2, а и б, очевидно, является трехмерный поворот, переводящий прибор S в положе­ние прибора Т. Когда матрица преобразования R ji зави­сит, как в нашем случае, только от поворота, ее называют матрицей поворота.

Для следующего шага нужно еще немного информации. Пусть мы добавили третий прибор (назовем его U ), стоящий вслед за Т под каким-то произвольным углом (фиг. 4.3, а).

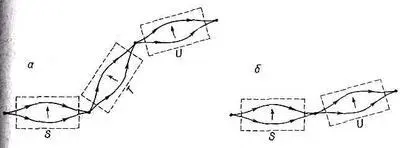
Фиг. 4.3. Если Т «открыт до отказа», то б эквивалентно а.

(Все это начинает выглядеть устрашающе, но в этом-то и прелесть отвлеченного мышления: самые сверхъестественные опыты можно ставить, просто проводя новые линии!) Что же пред­ставляет собой преобразование S ® Т ® U ? Фактически нас интересует амплитуда перехода из некоторого состояния по отношению к S к некоторому другому состоянию по отношению к U, если известны преобразования от S к Т и от Т к U, Поин­тересуемся сперва опытом, в котором в Т открыты оба канала. Ответ можно получить, дважды подряд применяя (4.5). Для перехода от S -представления к T -представлению имеем

где верхние индексы TS нужны, чтобы отличать это R от R UT , когда мы будем переходить от Т к U.

Обозначая амплитуды появления атома в базисных состоя­ниях представления U через C" k , можно связать их с T -амплитудами, применяя (4.5) еще раз; получим

Теперь можно из (4.6) и (4.7) получить преобразование от S прямо к U. Подставляя С' j из (4.6) в (4.7), имеем

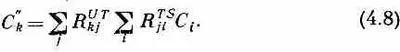
Или, поскольку в R UT kj отсутствует i, можно поставить сум­мирование по i впереди и написать

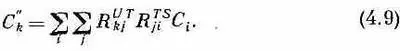
Это и есть формула двойного преобразования.

Заметьте, однако, что, пока пучки в Т не загораживаются, состояния на выходе из Т те же, что и при входе в него. Мы могли бы с равным успехом делать преобразования из S -представления прямо в представление U. Это значило бы, что прибор U по­ставлен прямо за S, как на фиг. 4.3, б. В этом случае мы бы написали

где R US ki — коэффициенты, принадлежащие этому преобразо­ванию. Но ясно, что (4.9) и (4.10) должны приводить к одинако­вым амплитудам С" k , причем независимо от того, каково было то начальное состояние j, которое снабдило нас амплитудами С i . Значит, должно быть

Иными словами, для любого поворота S®U базиса, если рас­сматривать его как два последовательных поворота S®Т и Т®U, можно получить матрицу поворота r us ki из матриц двух частных поворотов при помощи формулы (4.11). Если угод­но, (4.11) следует прямо из (4.1) и представляет собой лишь другую запись формулы: