Ричард Фейнман - 8. Квантовая механика I

Может быть, стоит подчеркнуть, что в то время, как про­странственные трехмерные векторы выражаются через три ортогональных единичных вектора, базисные векторы | i > квантовомеханических состояний должны пробегать всю совокуп­ность, отвечающую данной задаче. В зависимости от положения вещей в нее может входить два или три, пять или бесконечно много базисных состояний.

Мы говорили также о том, что происходит, когда частицы проходят через прибор. Если мы выпустим частицы в опре­деленном состоянии j, затем проведем их через прибор, а после проделаем измерение, чтобы посмотреть, находятся ли они в состоянии c, то результат будет описываться амплитудой

Такой символ не имеет близкого аналога в векторной алгебре. (Он ближе к тензорной алгебре, но эта аналогия не так уж полезна.) Мы видели в гл. 3 [формула (3.32)], что (6.16) можно переписать так:

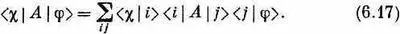
Это пример двукратного применения основного правила (6.9).

Мы обнаружили также, что если вслед за прибором А по ставить другой прибор 5, то можно написать

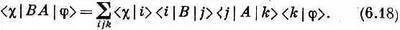
Это опять-таки следует прямо из предложенного Дираком метода записи уравнения (6,9). Вспомните, что между В и A всегда можно поставить черту (|), которая ведет себя совсем как множитель единица.

Кстати говоря, об уравнении (6.17) можно рассуждать и иначе. Предположим, что мы рассуждаем о частице, попадающей в прибор А в состоянии j и выходящей из него в состоянии y. Мы можем задать себе такой вопрос: можно ли найти такое состояние y, чтобы амплитуда перехода от y к c тождественно совпадала с амплитудой A |j>?Ответ гласит да. Мы хотим, чтобы (6.17) заменилось уравнением

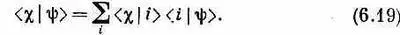
Конечно, этого можно достичь, если взять

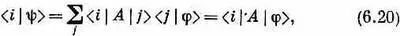
что и определяет собой y. «Но оно не определяет собой y,— скажете вы,— оно определяет только < i |y>». Однако все же определяет y; ведь если у вас есть все коэффициенты, связывающие y с базисными состояниями i , то y опреде­ляется однозначно. И действительно, можно поупражняться с нашими обозначениями и записать (6.20) в виде

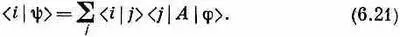
А раз это уравнение справедливо при всех г, то можно просто писать

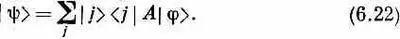
Теперь мы вправе сказать: «Состояние y — это то, что полу­чается, если начать с j и пройти сквозь аппарат A ».

Еще один, последний пример полезных уловок. Начинаем опять с (6.17). Раз это уравнение соблюдается при любых c и j, то их обоих можно сократить! Получаем

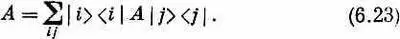
Что это значит? Только то, что получится, если вернуть на свои места j и c. В таком виде это уравнение «недокончено» и неполно. Если умножить его «справа» на |j>, то оно превра­щается в

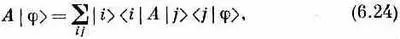
а это снова то же уравнение (6.22). В самом деле, мы бы могли просто убрать из (6.22) все j и написать

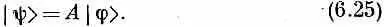
Символ А — это не амплитуда и не вектор; это вещь осо­бого рода, именуемая оператором. Он — нечто, что «опериру­ет» над состоянием, чтобы создать новое состояние; уравнение (6.25) говорит, что |y)> — это то, что получается, если А дей­ствует на |j>. Это уравнение тоже нужно считать недокончен­ным, открытым, пока слева оно не умножится на какое-то «брэ», скажем на

Оператор А, разумеется, полностью описывается тем, что за дается матрица амплитуд < i | A | j >;ее также пишут в виде А ij — через любую совокупность базисных векторов.

Все эти математические обозначения на самом деле ничего нового не вносят. Единственный резон, почему мы их ввели,— мы хотели показать, как пишутся обрывки уравнений, потому что во многих книжках вы встретите уравнения, написанные в неполном виде, и нет причин вам пугаться, увидев их. Если вы захотите, вы всегда сможете дописать те части, которых не хватает, и получить уравнение, связывающее числа. Оно будет выглядеть более привычно.

Кроме того, как вы увидите, обозначения «брэ» и «кет» очень удобны. Прежде всего мы теперь сможем указывать со­стояния, задавая их вектор состояния. Когда мы захотим вести речь о состоянии с определенным импульсом р, то скажем: «состояние

| р>». Или будем говорить о некотором произволь­ном состоянии |y>. Для единообразия мы всегда, говоря о состоянии, будем употреблять «кет» и писать |y>. (Конечно, этот выбор совершенно произволен; в равной мере мы могли бы остановиться и на «брэ»

§ 3. Каковы базисные состояния мира?

Мы обнаружили, что всякое состояние в мире может быть представлено в виде суперпозиции (линейной комбинации с подходящими коэффициентами) базисных состояний. Вы вправе спросить, во-первых: каких именно базисных состояний? Что ж, возможностей здесь немало. Можно, например, взять проек­цию спина на направление z или на некоторое другое направ­ление. Имеется очень-очень много различных представлений — аналогов различных систем координат, которые можно при­менять для представления обычных векторов. Затем можно спросить: с какими коэффициентами их брать? А это уж за­висит от физических обстоятельств. Различные совокупности коэффициентов отвечают разным физическим условиям. Здесь важно знать одну вещь — «пространство», в котором вы ра­ботаете, иными словами, знать, что эти базисные состояния означают физически. Так что первое, что вы, вообще говоря, должны знать,— это на что похожи базисные состояния. Тогда вам станет понятно, как описывать положение вещей на языке этих базисных состояний.