Ричард Фейнман - 8. Квантовая механика I

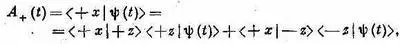
или

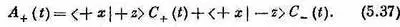
Опять пользуясь результатом последней главы (или лучше равенством

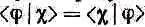* из гл. 3), мы пишем

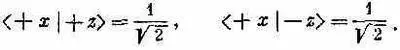
Итак, в (5.37) все известно. Мы получаем

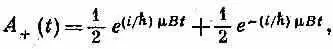
или

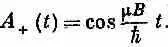
Поразительно простой результат! Заметьте: ответ согласуется с тем, что ожидалось при t= 0 . Мы получаем А + (0) = 1 , и это вполне правильно, потому что сперва и было предположено, что при t =0 мюон был в состоянии (+ x ).

Вероятность Р + того, что мюон окажется в состоянии (+х) в момент t, есть (А +) 2, т. е.

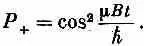
Вероятность колеблется от нуля до единицы, как показано на фиг. 5.10.

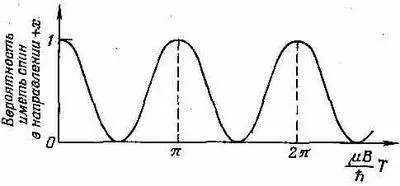
Фиг. 5.10. Временная зависимость вepo ятности того. что частица со спином 1 / 2 окажется в состоянии (+) по отношению оси х.

Заметьте, что вероятность возвращается к единице при m Bt/h=p (а не при 2p). Из-за того что косинус возведен в квадрат, вероятность повторяется с частотой 2mB/h.

Итак, мы обнаружили, что шанс поймать в электронном счетчике, показанном на фиг. 5.9, распадный электрон перио­дически меняется с величиной интервала времени, в течение которого мюон сидел в магнитном поле. Частота зависит от магнитного момента (Л. Именно таким образом и был на самом деле измерен магнитный момент мюона.

Тем же методом, конечно, можно воспользоваться, чтобы ответить на другие вопросы, касающиеся распада мюона. На­пример, как зависит от времени t шанс заметить распадный электрон в направлении у, под 90° к направлению х, но по-прежнему под прямым углом к полю? Если вы решите эту за­дачу, то увидите, что вероятность оказаться в состоянии (+у) меняется как cos 2 {(m Bt/h )-(p/4)}; она колеблется с тем же периодом, но достигает максимума на четверть цикла позже, когда mBt/h=p/4. На самом-то деле происходит вот что: с те­чением времени мюон проходит через последовательность со­стояний, отвечающих полной поляризации в направлении, ко­торое непрерывно вращается вокруг оси z. Это можно описать, говоря, что спин прецессирует с частотой

Вам должно становиться понятно, в какую форму выли­вается квантовомеханическое описание, когда мы описываем поведение чего-либо во времени.

* Если вы пропустили гл. 4, то можете пока просто считать (5.35) невыведенным правилом. Позже, в гл. 8, мы разберем прецессию спина подробнее, будут получены и эти амплитуды.

* Мы предполагаем, что фазы обязаны иметь одно и то же значение в соответствующих точках в двух системах координат. Впрочем, это весьма тонкое место, поскольку в квантовой механике фаза в значитель­ной степени произвольна. Чтобы до конца оправдать это предположение, нужны более детальные рассуждения, учитывающие интерференцию двух или нескольких амплитуд.

§ 1. Амплитуды и векторы

§ 2. Разложение век­торов состояний

§ 3. Каковы базисные состояния мира?

§ 4. Как состояния меняются во времени

§ 5. Гамильтонова матрица

§ б. Молекула аммиака

Повторить: гл. 49) (вып. 4) «Собст­венные колеба­ния»

§ 1. Амплитуды и векторы

Прежде чем приступить к основной теме этой главы, мы хотели бы изложить несколько математических идей, которые часто встреча­ются в книгах по квантовой механике. Знание их облегчит вам чтение других книг или статей по этому предмету. Первая идея — это тесное математическое подобие между уравнениями квантовой механики и формулами для скаляр­ного произведения двух векторов. Вы помните, что если c и j — два состояния, то амплитуда начать в j и кончить в c может быть записана в виде суммы (по полной совокупности базис­ных состояний) амплитуд перехода из j в одно из базисных состояний и затем из этого базис­ного состояния уже в c:

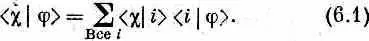
Мы объясняли это при помощи прибора Штер­на — Герлаха, но сейчас напоминаем вам, что в этих приборах нет нужды. Уравнение (6.1) — это математический закон, который верен всег­да, все равно, есть ли у нас фильтровальное оборудование или нет; вообще совсем не обя­зательно воображать наличие какого-то при­бора. Можно рассматривать это просто как формулу для амплитуды .

Сопоставим (6.1) с формулой для скалярного произведения двух векторов В и А. Если В и А — обычные трехмерные векторы, то ска­лярное произведение можно написать так:

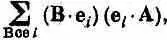
считая, что символ е iобозначает любой из трех единичных векторов в направлениях х.у и z. Тогда B·e 1 — это то, что обычно называют В х , а В·е 2 — то, что обычно называют B y , и т,д. Значит, (6.2) эквивалентно

В х А х +В у А у +В г А г ,

а это и есть скалярное произведение В·А.

Сравнение (6.1) с (6.2) обнаруживает следующую аналогию. Состояния c и j соответствуют двум векторам А и В. Базис­ные состояния i отвечают специальным векторам е i, к которым мы относим все прочие векторы. Любой вектор может быть представлен как линейная комбинация трех «базисных векто­ров» е i. Далее, если вам известны коэффициенты при каждом «базисном векторе» в этой комбинации, т. е. три его компонен­ты, то вы знаете о векторе все. Точно так же любое квантовомеханическое состояние может быть полностью описано ампли­тудами < i |j> перехода в базисные состояния, и если эти коэф­фициенты вам известны, то вы знаете все, что можно знать о состоянии. Из-за этой тесной аналогии то, что мы назвали «состоянием», часто именуют «вектором состояния».