Ричард Фейнман - 7. Физика сплошных сред

Посмотрим, что получится, если мы приложим к чему-то «косое» напряжение. Под косым, или скалывающим, напряже­нием мы подразумеваем такое воздействие, как показано на фиг. 38.4.

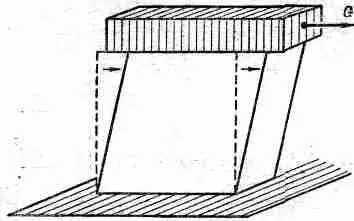
Фиг. 38.4. Однородный сдвиг.

В качестве предварительной задачи посмотрим, ка­кова будет деформация кубика под действием сил, показанных на фиг. 38.5.

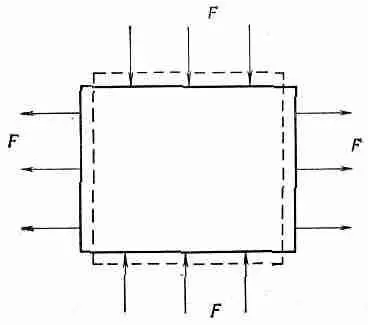
Фиг. 38.5. Действие сжи­мающих сил, давящих на вершину и основание, и рав­ных им растягивающих сил с двух сторон.

Снова можно разделить эту задачу на две: вер­тикальное давление и горизонтальное растяжение. Обозначая через А площадь грани кубика, мы получаем для изменения горизонтальной длины

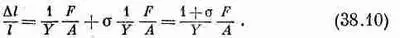
Изменение же высоты по вертикали равно просто тому же выражению с обратным знаком.

Предположим те­перь, что мы имеем тот же самый кубик, и под­вергнем его действию сдвиговых сил, показанных на фиг. 38.6, а.

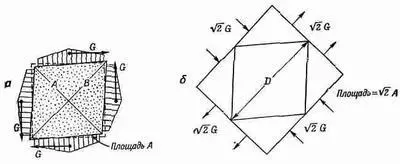
Фиг. 38.6. Две пары сил сдвига (а) создают то же самое напряжение, что и сжимающие = растягивающие силы (б).

Заметим те­перь, что все силы должны быть равными, ибо на тело не должен действовать никакой момент сил и оно должно находиться в равновесии. (Подобные силы должны дей­ствовать также и в случае, изображенном на фиг. 38.4, поскольку кубик находится в равновесии. Они обеспечиваются тем, что кубик «приклеен» к столу.) При таких условиях го­ворят, что кубик находится в состоянии чистого сдвига. Но об­ратите внимание, что если мы разрежем кубик плоскостями под углом 45°, скажем, вдоль диагонали А на фиг. 38.6, а, то полная сила, действующая в этой плоскости, нормальна к ней и равна Ц2G.Площадь, на которой действует эта сила, равна Ц2A;следовательно, напряжение, нормальное к этой плоско­сти, будет просто G/A. Точно так же если взять плоскость, наклоненную под углом 45° в другую сторону, т. е. по диа­гонали В, то мы увидим, что на ней действует нормальное сдавливающее напряжение, равное - G/A. Из этого ясно, что напряжение при «чистом сжатии» эквивалентно комби­нации растягивающего и сжимающего напряжений, направлен­ных под прямым углом друг к другу и под углом 45° к перво­начальным граням кубика. Внутренние напряжения и деформа­ции будут такими же, как и в большом кубике материала под действием сил, показанных на фиг. 38.6, б. Но эту задачу мы уже решили. Изменение длины диагонали задается уравнением (38.10):

(Одна диагональ сокращается, а другая удлиняется.)

Часто деформацию сдвига удобно описывать с помощью угла «искажения» кубика q, показанного на фиг. 38.7.

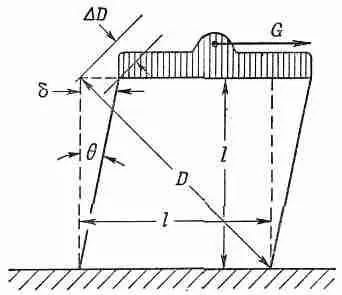
Фиг. 38.7. Напряжение сдвига q равно 2DD/D.

Из геометрии фигуры вы видите, что горизонтальный сдвиг б верхнего края равен Ц 2DD, так что

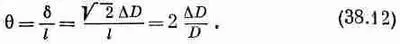
Напряжение сдвига g определяется как отношение тангенциаль­ной силы, действующей на грань, к площади грани g=G/A. Воспользовавшись уравнением (38.11), мы из (38.12) получаем

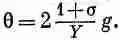
Или, если написать это в форме

Напряжение = ПостояннаяXДеформация

g=mq. (38.13)

Коэффициент пропорциональности m называется модулем сдвига (или иногда коэффициентом жесткости). Вот как он выражается через Y и s:

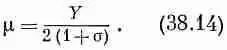
Кстати, модуль сдвига дол­жен быть положительным, иначе мы бы могли полу­чить энергию от самопро­извольного сдвига кубика. Из уравнения (38.14) очевидно, что постоянная а должна быть больше -1. Теперь мы знаем, что о заключена между -1 и 1/ 2, но на практике, однако, она всегда больше нуля. В ка­честве последнего примера состояний подобного типа, когда напряженность постоянна по всему материалу, давайте рассмот­рим задачу о бруске, который растягивается и в то же время закреплен таким образом, что боковое сокращение невозможно. (Технически немного легче сжимать брусок и сдерживать бока его от «распирания», но в сущности — это та же самая за­дача.) Что при этом происходит? На брусок должны действо­вать боковые силы, которые препятствуют изменению его тол­щины,— силы, которых мы не знаем непосредственно, но ко­торые следует вычислить. Эта задача того же самого сорта, что мы решали, но только с немного другой алгеброй. Представьте себе силы, действующие на все три стороны, как это показано на фиг. 38.8.

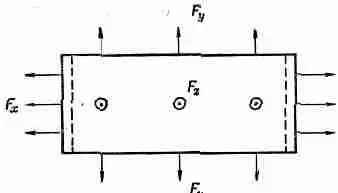
Фиг. 38.8. Растяжение без сокращения бокового размера.

Мы вычислим изменение размеров и подберем та­кие поперечные силы, чтобы ширина и высота оставались по­стоянными. Следуя обычным рассуждениям, мы получаем для трех напряжений

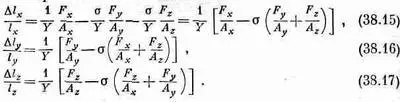
Но поскольку по условию Dl уи Dl z равны нулю, то уравнения (38.16) и (38.17) дают два соотношения, связыва­ющие F y и F z с F x . Совместно решая их, найдем

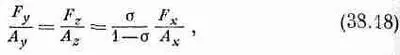
а подставляя (38.18) в (38.15), получаем

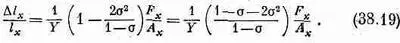
Это соотношение вы часто можете встретить «перевернутым» и с преобразованным квадратичным полиномом по s, т. е.

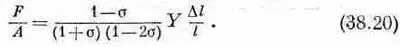
Когда вы удерживаете бока, модуль Юнга умножается на не­которую сложную функцию s. Из уравнения (38.19) можно сразу же увидеть, что множитель перед Y всегда больше едини­цы. Растянуть брусок, когда его бока удерживаются, гораздо труднее. Это означает также, что брусок становятся жестче, когда его боковые стороны закреплены, нежели когда они свободны.