Ричард Фейнман - 7. Физика сплошных сред

Согласно (38.34), dF=Y(y/R)dA, так что

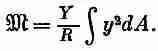
Но интеграл от y 2 dA можно назвать «моментом инерции» гео­метрического поперечного сечения относительно горизонталь­ной оси, проходящей через его «центр масс»; мы будем обоз­начать его через I , т. е.

Уравнение (38.36) дает нам соот­ношение между изгибающим момен­том 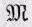и кривизной балки 1/R. «Жесткость» балки пропорциональна Y и моменту инерции I . Другими словами, если вы хотите какую-то балку, скажем из алюминия, сделать как можно жестче, то вы должны как можно больше вещества поме­стить как можно дальше от оси, относительно которой берется момент инерции. Но этого нельзя доводить до предела, ибо тогда балка не будет искривляться так, как мы предположили: она согнется или скрутится и снова станет слабее. Вот почему каркасные балки делают в форме буквы I или Н (фиг. 38.13).

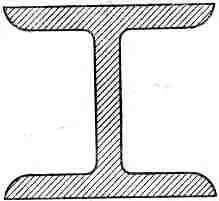
Фиг. 38.13. Двутавровая балка.

В качестве примера применения нашего уравнения (38.36) для балки вычислим отклонение консольной балки под дейст­вием сосредоточенной силы W, действующей на ее свободный конец (фиг. 38.14).

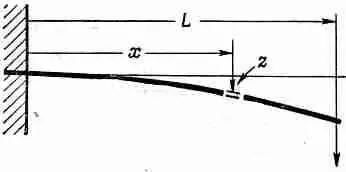
Фиг. 38.14. Консольная балка с нагрузкой на конце.

(Консольная балка закреплена одним концом, который вмурован в стенку.) Какая же тогда будет форма балки? Обозначим отклонение на расстоянии х от зак­репленного конца через z; мы хотим найти z(x). Будем вычис­лять только малые отклонения. Как вы знаете из курса мате­матики, кривизна 1/R любой кривой z(x) задается выражением

Нас интересуют только малые изгибы (обычная вещь в ин­женерных конструкциях), поэтому квадратом производной (dz/dx) 2 можно пренебречь по сравнению с единицей и считать

Нам нужно еще знать изгибающий момент 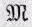. Он является функцией от х, так как в любом поперечном сечении он равен моменту относительно нейтральной оси. Весом самой балки пренебрежем и будем учитывать только силу W, действующую вниз на свободный ее конец. (Если хотите, можете сами учесть ее вес.) При этом изгибающий момент на расстоянии х равен

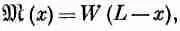
ибо это и есть момент сил относительно точки х, с которым действует груз W, т. е. груз, который должен поддерживать балку. Получаем

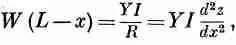
или

Это уравнение можно проинтегрировать без всяких фокусов и получить

воспользовавшись предварительно нашим предположением, что z(0)=0 и что dz/dx в точке x=0 тоже равно нулю. Это и есть граничные условия. А отклонение конца будет

т, е. отклонение возрастает пропорционально кубу длины балки. При выводе нашей приближенной теории мы предполагали, что при изгибании поперечное сечение бруска не изменяется. Когда толщина бруска мала по сравнению с радиусом кривизны, поперечное сечение изменяется очень мало и все отлично. Однако в общем случае этим эффектом пренебречь нельзя — согните пальцами канцелярскую резин­ку и вы сами убедитесь в этом. Если первоначально попереч­ное сечение было прямоуголь­ным, то, согнув резинку, вы уви­дите, как она выпирает у основания (фиг. 38.15).

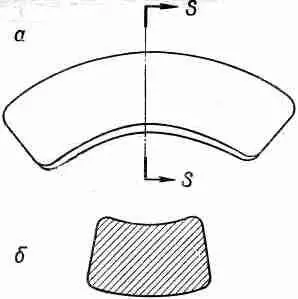
Фиг. 38.15. Согнутая резинка (а) и ее поперечное сечение (б).

Это получается потому, что, согласно отноше­нию Пуассона, при сжатии основания материал «раздается» вбок. Резинку очень легко согнуть или растянуть, но она несколько напоминает жидкость в том отношении, что изменить ее объем очень трудно. Это и сказывается при сгибании резинки. Для несжимаемых материалов отношение Пуассона было бы точно равно 1/ 2, для резинки те оно близко к этому числу.

§ 5. Продольный изгиб

Теперь воспользуемся нашей теорией, чтобы понять, что про­исходит при продольном изгибе бруска, опоры или стержня. Рассмотрим то, что изображено на фиг. 38.16.

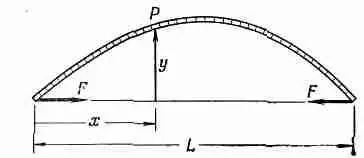
Фиг. 38.16. Продольно изогну­тая балка.

Здесь стержень, обычно прямой, удерживается в согнутом виде двумя проти­воположными силами, давящими на его концы. Найдем форму стержня и величину сил, действующих на концы.

Пусть отклонение стержня от прямой линии между концами будет у(х), где х — расстояние от одного конца. Изгибающий момент в точке Р на рисунке равен силе F, умноженной на плечо, перпендикулярное направлению у:

Воспользовавшись выражением для момента (38.36), имеем

При малых отклонениях можно считать 1 /R=-d 2 y/dx 2 (от­рицательный знак выбран потому, что кривизна направлена вниз). Отсюда