Ричард Фейнман - 6a. Электродинамика

Можно, хотя и не легко, вычислить эту силу самодействия, однако здесь мы не будем заниматься такими трудоемкими рас­четами. Я просто скажу вам, что получается в специальном сравнительно простом случае движения в одном измерении, скажем вдоль оси х. Самодействие в этом случае можно записать в виде ряда. Первый член этого ряда зависит от ускорений х, следующий — пропорционален х и т. д.

Так что в результате

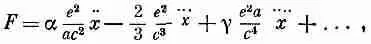
(28.9)

где a и g — числовые коэффициенты порядка единицы. Коэффи­циент ос при слагаемом x зависит от предположенного распреде­ления зарядов; если заряды равномерно распределены по сфере, то a= 2/ 3. Таким образом, слагаемое, пропорциональное ускоре­нию, изменяется обратно пропорционально радиусу электрона а, что в точности согласуется с величиной, полученной для m эм в (28.4). Если взять другое распределение, то а изменится, но в точности так же изменится и величина 2/ 3в (28.4). Слагаемое с х не зависит ни от радиуса а, ни от предположенного распре­деления заряда; коэффициент при нем всегда равен 2/ 3. Следую­щее слагаемое пропорционально радиусу а и коэффициент g при нем определяется распределением заряда. Обратите внима­ние, что если устремить радиус электрона к нулю, то последнее слагаемое (равно как и все высшие члены) обратится в нуль, второе остается постоянным, но первое — электромагнитная масса — становится бесконечным. Видно, что бесконечность возникает из-за действия одной части электрона на другую; по-видимому, мы допустили глупость — возможность «точеч­ного» электрона действовать на самого себя.

§ 5. Попытки изменения теории Максвелла

Теперь мне бы хотелось обсудить, как можно изменить электродинамику Максвелла, но изменить так, чтобы сохранить понятие простого точечного заряда. В этом направлении было сделано немало попыток, а некоторые теории сумели даже так представить дело, что вся масса электрона оказалась полностью электромагнитной. Однако ни одной из этих теорий не суждено было выжить. И все же интересно обсудить некоторые из пред­ложенных возможностей хотя бы для того, чтобы оценить борь­бу человеческого разума.

Наша теория электромагнетизма началась с разговоров о взаимодействии одного заряда с другим. Затем мы построили теорию этих взаимодействующих зарядов и закончили наше изу­чение теорией поля. Мы настолько уверовали в нее, что пытались с ее помощью определить, как одна часть электрона действует на другую. Все трудности, возможно, происходят из-за того, что электрон не действует сам на себя; экстраполяция закона вза­имодействия между отдельными электронами на взаимодействие электрона самого с собой, возможно, ничем не оправдана. По­этому некоторые из предложенных теорий совсем исключают возможность самодействия электрона. Из-за этого в них уже не возникает бесконечностей. И никакой электромагнитной массы при этом у частиц нет, а ее масса снова полностью механическая. Однако в такой теории возникают новые трудности.

Нужно сразу же вам сказать, что такие теории требуют из­менения и понятий электромагнитного поля. Как вы помните, мы говорили, что сила, действующая на частицу в любой точке, определяется просто двумя величинами: Е и В. Если мы отказываемся от идеи самодействия, то это утверждение становится уже несправедливым, ибо силы, действующие на электрон в некотором месте, больше не определяются полями Е и В, а только теми их частями, которые создаются другими зарядами. Так что мы всегда должны помнить о том, какие поля Е и В создает тот заряд, для которого вычисляется действующая сила, а какие — все остальные заряды. Это делает теорию гораздо более запутанной, хотя и позволяет избежать трудностей с бесконечностями.

Итак, если нам очень хочется, мы можем выбросить весь набор сил в уравнении (28.9), приговаривая при этом, что такое явление, как действие электрона на себя, отсутствует. Но вместе с водой мы выплескиваем и ребенка! Ведь второе-то слагаемое в (28.9), слагаемое с х, совершенно необходимо. Эта сила приво­дит к вполне определенному эффекту. Если вы ее выбросите — беды не миновать. Когда вы разгоняете заряд, он излучает элек­тромагнитные волны, т. е. теряет энергию. Поэтому ускорение заряда требует большей силы, чем ускорение нейтрального объекта той же массы; в противном случае энергия не будет со­храняться. Скорость, с которой мы затрачиваем работу на уско­рение заряда, должна быть равна скорости потери энергии на излучение. Мы уже говорили об этом эффекте; он был назван радиационным сопротивлением. Снова перед нами вопрос: от­куда берутся те дополнительные силы, на преодоление которых затрачивается эта работа? Когда излучает большая антенна, то эти силы возникают под влиянием токов одной ее части на токи в другой. Но у отдельного ускоряющегося электрона, излуча­ющего в пустое пространство, возможен только один источник таких сил — действие одной части электрона на другую.

В гл. 32 (вып. 3) мы обнаружили, что осциллирующий заряд излучает энергию со скоростью

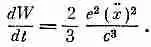
(28.10)

Давайте посмотрим, какая мощность необходима для преодоле­ния силы самодействия (28.9). Мощность, как известно, равна силе, умноженной на скорость, т. е. Fx:

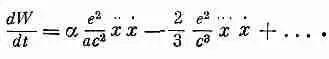
(28.11)

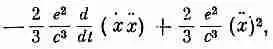
Первый член пропорционален dx 2 /dt и поэтому соответствует скорости изменения кинетической энергии 1/ 2mv 2, связанной с электромагнитной массой. А второй соответствует излучению мощности (28.10). Однако он отличается от (28.10). Разница состоит в том, что (28.11) справедливо в общем случае, тогда как (28.10) верно только для осциллирующего заряда. Мы можем доказать, что эти два выражения для периодического движения заряда эквивалентны. Перепишем для этого второй член выра­жения (28.11) в виде

что будет просто алгебраическим преобразованием. Если дви­жение электрона периодическое, то величина хх периодически возвращается к одному и тому же значению. Так что если мы возьмем среднее значение ее производной по времени, то получим нуль. Однако второй член всегда положителен (как квадрат величины), так что его производная тоже положительна. Соот­ветствующая ему мощность как раз равна выражению (28.10).