Ричард Фейнман - 6a. Электродинамика

(Интеграл, разумеется, должен браться по четырехмерному объему dt z dx z dy 2 dz 2 .)

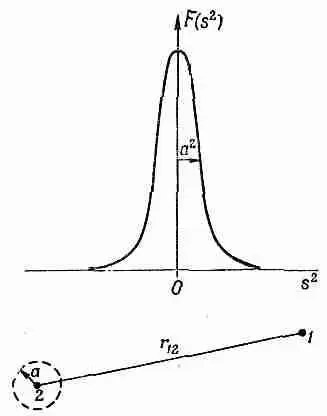
Фиг. 28,4. Функция F(s 2), ис­пользуемая в нелокальной теории Боппа.

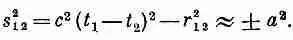
Теперь остается только выбрать подходящую функ­цию F. Относительно нее мы предполагаем только одно, что она повсюду мала, за исключением области аргу­мента вблизи нуля, т. е. что график F ведет себя подобно кривой, изображенной на фиг. 28.4. Это узкий пик в окрестности s 2=0, шириной которого грубо можно считать величину а 2. Если вычисляется потенциал в точке 1, то при­ближенно можно утверждать, что заметный вклад дают только те точки 2, для которых s 2 12= с 2(t 2-t 1 ) 2 -r 2 12отличается от нуля на ±a 2. Это можно выразить, сказав, что F важно только для

(28.16)

Если понадобится, можно проделать все математически более строго, но идея вам уже ясна.

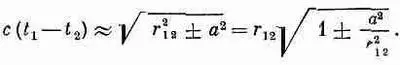
Предположим теперь, что а очень мало по сравнению с размерами обычных объектов типа электромоторов, генераторов и тому подобное, поэтому для обычных задач г 12>>а. Тогда вы­ражение (28.16) говорит, что в интеграл (28.15) дают вклад только те токи, для которых t 1-t 2очень мало:

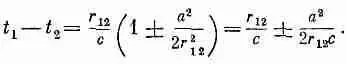
Но поскольку а 2/r 2 12<<1, то квадратный корень приближенно равен 1 ±а 2/2r 2 12, так что

В чем здесь суть? Полученный результат говорит, что для А m . в момент t 1 важны только те времена t 2, которые отличаются от него на запаздывание r 12/c с пренебрежимо малой поправкой, ибо r 1 2>>а. Другими словами, теория Боппа переходит в теорию Максвелла при удалении от зарядов в том смысле, что она при­водит к эффекту запаздывания.

Мы можем приближенно увидеть, к чему нас приведет инте­грал (28.15). Если, зафиксировав r 12, провести интегрирование по t 2 в пределах от -Ґ до +Ґ,то s 2 12тоже будет изменяться от -Ґ до +Ґ. Но основной вклад даст участок по t 2 шириной At 2=2·а 2/2r 12с с центром в момент t 1-r 12/c.Пусть функция F (s 2) при s 2=0 принимает значение К, тогда интегрирование по t 2 дает приблизительно Kj mDt 2, или

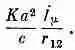
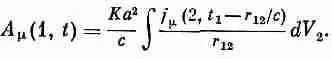
Разумеется, величину j mследует взять в момент t 2=t 1-r 12/c, так что (28.15) принимает вид

Если выбрать K=q 2с/4pe 0а 2, то мы придем прямо к запаздыва­ющему решению уравнений Максвелла для потенциалов, при­чем автоматически возникает зависимость 1/r! И все это получи­лось из простого предположения, что потенциал в одной точке пространства-времени зависит от плотности токов во всех других точках пространства-времени с весовым множите­лем, в качестве которого взята некая функция четырехмерного расстояния между двумя точками. Эта теория тоже дает конеч­ную электромагнитную массу электрона, а соотношение между энергией и массой как раз такое, какое требуется в теории относительности. Ничего другого не могло и быть, ибо теория релятивистски инвариантна с самого начала.

Однако и этой теории и всем другим описанным нами тео­риям можно предъявить тяжкое обвинение. Все известные нам частицы подчиняются законам квантовой механики, поэтому необходима квантовомеханическая форма электродинамики. Свет ведет себя подобно фотонам. Это уже не

100-процентная теория Максвелла. Следовательно, электродинамика должна быть изменена. Мы уже говорили, что упорное старание испра­вить классическую теорию может оказаться напрасной тратой времени, ибо в квантовой электродинамике трудности могут исчезнуть или будут разрешены другим образом. Однако и в квантовой электродинамике трудности не исчезают. В этом кроется одна из причин, почему люди потратили столько времени, пытаясь преодолеть классические трудности и надеясь, что если они смогут преодолеть их, то после квантового обоб­щения уравнений Максвелла все будет в порядке. Однако и после такого обобщения трудности не исчезают.

Квантовые эффекты, правда, приводят к некоторым измене­ниям. Изменяется формула для масс, появляется постоянная Планка h , но ответ по-прежнему выходит бесконечным, если вы не обрезаете как-то интегрирование, подобно тому как мы обре­зали интеграл при r =а в классической теории. Ответ при этом зависит от характера обрезания. К сожалению, я не могу вам показать, что трудности в основном те же самые, ибо вы еще слишком мало знаете о квантовой механике, а о квантовой элек­тродинамике — и того меньше. Поэтому вам придется поверить мне на слово, что и квантовая электродинамика Максвелла при­водит к бесконечной массе точечного электрона.

Оказывается, однако, что до сих пор никому не удалось даже приблизиться к самосогласованному квантовому обобще­нию на основе любой из модифицированных теорий. Идее Борна и Инфельда никогда не суждено было стать квантовой теорией. Не привели к удовлетворительной квантовой теории опережа­ющие и запаздывающие волны Дирака и Уилера — Фейнмана. Не привела к удовлетворительной квантовой теории и идея Боппа. Так что и до сего дня нам не известно решение этой проблемы. Мы не знаем, как с учетом квантовой механики по­строить самосогласованную теорию, которая не давала бы бес­конечной собственной энергии электрона или какого-то другого точечного заряда. И в то же время нет удовлетворительной тео­рии, которая описывала бы неточечный заряд. Так эта проблема и осталась нерешенной.

Если вы вздумаете попытать счастья и построить теорию, полностью удалив действие электрона на себя, так чтобы электромагнитная масса не имела смысла, а затем будете делать из нее квантовую теорию, то могу вас заверить — трудностей вы не избежите. Экспериментально доказано существование электромагнитной инерции и тот факт, что часть массы заряжен­ных частиц — электромагнитная по своему происхождению.

В старых книгах часто утверждалось, что поскольку при­рода не подарила нам двух одинаковых частиц, из которых одна нейтральная, а другая заряженная, то мы никогда не сможем сказать, какая доля массы является электромагнитной, а какая механической. Однако оказалось, что природа все же была достаточна щедра и подарила нам именно два таких объекта, так что, сравнивая наблюдаемую массу заряженной частицы с мас­сой нейтральной, мы можем сказать, существует ли электромаг­нитная масса. Возьмем, например, нейтрон и протон. Они взаи­модействуют с огромной силой — ядерной силой, детали происхождения которой нам неизвестны. Однако, как мы уже говорили, ядерные силы обладают одним замечательным свой­ством. По отношению к этим силам нейтрон и протон в точности одинаковы. Насколько мы сейчас можем судить, ядерные силы между двумя нейтронами, нейтроном и протоном и двумя протонами совершенно одинаковы. Отличаются эти частицы только сравнительно слабыми электромагнитными силами; по отноше­нию к ним протон и нейтрон отличаются, как день и ночь. Вот это нам как раз и нужно. Итак, мы имеем две частицы, одина­ковые с точки зрения сильных взаимодействий и различных с точки зрения электрических. И они имеют небольшую разницу в массах. Разница масс между протоном и нейтроном, выражен­ная в единицах энергии покоя mc 2 , составляет 1,3 Мэв, что со­ответствует 2,6 электронным массам. Классическая теория пред­сказывает для радиуса протона величину между 1/ 3и 1 / 2 ра­диуса электрона, или около 10 -1 3 см. Конечно, на самом деле следует пользоваться квантовой теорией, но по какой-то стран­ной случайности все константы, 2p, h , и т. д., комбинируются так, что приблизительно дают тот же самый результат, что и классическая теория. Одна беда: знак оказывается неверным! Нейтрон на самом деле тяжелее протона.