Ричард Фейнман - 6a. Электродинамика

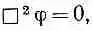
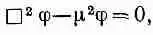
где j может быть каким-то другим четырехвектором или, возможно, скаляром. Далее выяснилось, что у p-мезона никакой поляризации нет, поэтому j должно быть скаляром. Согласно этому простому уравнению, мезонное поле должно изменяться с расстоянием от источника как 1/r 2, т. е. в точности как элект­рическое. Однако мы знаем, что радиус действия ядерных сил гораздо меньше, чего не может обеспечить нам это простое урав­нение. Есть только один способ изменить положение вещей, не разрушая релятивистской инвариантности,— добавить или вы­честь из даламбертиана произведение константы на поле j. Итак, Юкава предположил, что свободные кванты ядерных сил могут подчиняться уравнению

(28.17)

где m 2— некоторая постоянная, т. е. какой-то скаляр. (Посколь­ку  2является скалярным дифференциальным оператором, то инвариантность не нарушится, если мы добавим к нему дру­гой скаляр.)

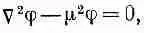
Давайте посмотрим, что дает уравнение (28.17), когда ядер­ные силы не изменяются с течением времени. Мы хотим найти решение уравнения

которое было бы сферически симметрично относительно неко­торой точки, скажем относительно начала координат. Если j зависит только от r, то мы знаем, что

Таким образом, получается уравнение

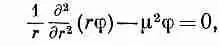
или

Рассматривая теперь произведение (rj) как новую функцию, мы имеем для нее уравнение, которое встречалось нам уже много раз. Решение ее имеет вид

Ясно, что при больших r поле j не может быть бесконеч­ным, поэтому нужно отбросить знак плюс в показателе экспо­ненты, после чего решение примет вид

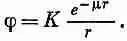
(28.18)

Эта функция называется потенциалом Юкавы. Для сил притя­жения К должно быть отрицательным числом, величина которо­го подбирается так, чтобы удовлетворить экспериментально наблюдаемой величине ядерных сил.

Потенциал Юкавы благодаря экспоненциальному множителю угасает быстрее, чем 1/r. Как это видно из фиг. 28.6, для рас­стояний, превышающих 1/m, потенциал, а следовательно, и ядерные силы приближаются к нулю гораздо быстрее, чем 1/r. Поэтому «радиус действия» ядерных сил гораздо меньше «радиуса действия» электростатических. Экспериментально дока­зано, что ядерные силы не простираются на расстояния свыше 10 -1 3 см, поэтому

m»10 15 м -1 .

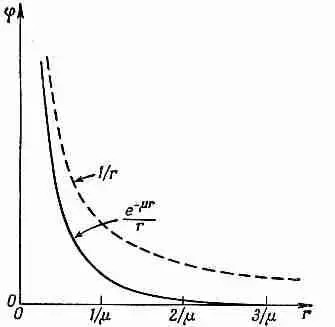
Фиг. 28.6. Сравнение потенциала Юкавы. е - m r / r с кулоновым потен­циалом 1/r.

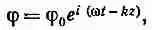
И, наконец, давайте рассмотрим волновое решение уравне­ния (28.17). Если мы подставим в него

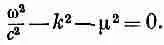
то получим

Связывая теперь частоту с энергией, а волновое число с импуль­сом, как это делалось в конце гл. 34 (вып. 3), мы найдем соот­ношение

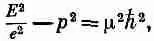
которое говорит, что масса «фотона» Юкавы равна m h/с. Если в качестве m взять величину ~10 15м -1, которую дает наблюдаемый радиус действия ядерных сил, то масса оказывается равной 3·10 -2 5г, или 170 Мэв, что приблизительно равно наблюдаемой массе p-мезона. Таким образом, по аналогии с электродинами­кой мы бы сказали, что p-мезон — это «фотон» поля ядерных сил. Однако теперь мы распространили идеи электродинамики в такую область, где они на самом деле могут оказаться и не­верными. Мы вышли далеко за рамки электродинамики и очутились перед проблемой ядерных сил.

* Мы пользуемся такими обозначениями x=dx/dt, x=d 2 x/dt 2 , x=d 3 x/dt 3 и т. д.

§ 1. Движение в однородных электрическом я магнитном полях

§ 2. Анализатор импульсов

§ 3. Электростатиче­ская линза

§ 4. Магнитная линза

§ 5. Электронный микроскоп

§ 6. Стабилизирую­щие поля ускори­телей

§ 7. Фокусировка чередующимся градиентом

§ 8. Движение в скрещенных электрическом и магнитном полях

Повторить: гл. 30 (вып. 3) «Дифракция».

§ 1. Движение в однородных электрическом и магнитном полях

Мы теперь перейдем к описанию в общих чер­тах движения зарядов в различных условиях. Наиболее интересные явления возникают тогда, когда зарядов движется много и все они взаимо­действуют друг с другом. Так обстоит дело, когда электромагнитные волны проходят через кусок вещества или плазму; тогда легионы за­рядов взаимодействуют друг с другом. Но это очень сложная картина. Позднее мы поговорим и о таких проблемах; пока же мы обсудим не­сравненно более простую задачу о движении отдельного заряда в заданном поле. При этом можно пренебречь всеми другими зарядами, за исключением, разумеется, тех зарядов и токов, которые создают предполагаемое нами поле.

Начать, по-видимому, нужно с движения частицы в однородном электрическом поле. Движение при небольших скоростях не пред­ставляет особенного интереса — это просто рав­номерно ускоренное движение в направлении поля. А вот когда частица, набрав достаточно энергии, превращается в релятивистскую, дви­жение ее становится более сложным. Решение для этого случая я оставляю вам — потруди­тесь и отыщите его сами.

Мы же рассмотрим движение в однородном магнитном поле, когда электрического поля нет. Эту задачу мы уже решали. Одним из ре­шений было движение частиц по окружности. Магнитная сила