Ричард Фейнман - 6. Электродинамика

*Это не совсем так. Поля могут быть «поглощены», если попадут в область, в которой есть заряды.

Это значит, что где-то могут быть созданы другие поля, которые наложатся на эти поля и «погасят»их в результате деструктивной интерференции (см. гл. 31, вып. 3)

* К-2— вторая по высоте вершина мира в северо-западных отрогах Гималаев, называемых Каракорум.—- Прим. ред.

*Выбор значения С·А называется «выбором калибровки». Изменение А за счет добавления Сy называется «калибровочным преобра­зованием». Выбор (18.23) называют «калибровкой Лоренца».

Добавление, сделанное после лекции

Когда я учился в школе, наш учитель фи­зики, по фамилии Бадер, однажды зазвал меня к себе после урока и сказал: «У тебя вид такой, как будто тебе все страшно надоело; послу­шай-ка об одной интересной вещи». И он рас­сказал мне нечто, что мне показалось поистине захватывающим. Даже сейчас, хотя с тех пор прошла уже уйма времени, это продолжает меня увлекать. И всякий раз, когда я вспоми­наю о сказанном, я вновь принимаюсь за ра­боту. И на этот раз, готовясь к лекции, я поймал себя на том, что вновь анализирую все то же самое. И, вместо того чтобы гото­виться к лекции, я взялся за решение новой задачи. Предмет, о котором я говорю,— это принцип наименьшего действия.

Вот что сказал мне тогда мой учитель Бадер: «Пусть, к примеру, у тебя имеется частица в поле тяжести; эта частица, выйдя откуда-то, свободно движется куда-то в другую точку. Ты подбросил ее, скажем, кверху, а она взлетела, а потом упала.

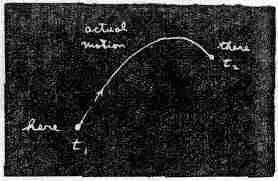
От исходного места к конеч­ному она прошла за какое-то время. Попробуй теперь какое-то другое движение. Пусть для того, чтобы перейти «отсюда сюда», она двигалась уже не так, как рань­ше, а вот так:

но все равно очутилась на нужном месте в тот же самый момент вре­мени, что и раньше».

«И вот,— продолжал учитель,— если ты подсчитаешь кине­тическую энергию в каждый момент времени на пути частицы, вычтешь из нее потенциальную энергию и проинтегрируешь разность по всему тому времени, когда происходило движение, то увидишь, что число, которое получится, будет больше, чем при истинном движении частицы.

Иными словами, законы Ньютона можно сформулировать не в виде F=ma, а вот как: средняя кинетическая энергия минус средняя потенциальная энергия достигает своего самого наи­меньшего значения на той траектории, по которой предмет двигается в действительности от одного места к другому.

Попробую пояснить тебе это чуть понятнее.

Если взять поле тяготения и обозначить траекторию час­тицы x(t), где х — высота над землей (обойдемся пока одним измерением; пусть траектория пролегает только вверх и вниз, а не в стороны), то кинетическая энергия будет 1/ z m(dx/dt) 2 , а потенциальная энергия в произвольный момент времени будет равна mgx.

Теперь я для какого-то момента движения по траектории беру разность кинетической и потенциальной энергий и интегри­рую по всему времени от начала до конца. Пусть в начальный момент времени t t движение началось на какой-то высоте, а кончилосъ в момент t 2на дру­гой определенной высоте.

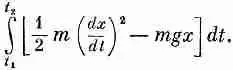
Тогда интеграл равен

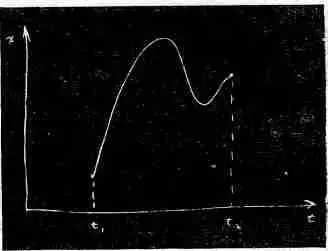
Можно подсчитать раз­ность потенциальной и кинетической энергий на таком пути... или на любом другом. И самое поразительное — что настоящий путь это тот, по которому этот интеграл наименьший.

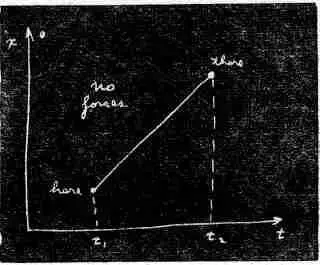
Давай проверим это. Для начала разберем такой случай: у свободной частицы вовсе нет потенциальной энергии. Тогда правило говорит, что при переходе от одной точки к другой за заданное время интеграл от кинетической энергии должен оказаться наименьшим. А это значит, что частица обязана дви­гаться равномерно. (И это правильно, мы же с тобой знаем, что скорость в таком движении постоянна.) А почему равно­мерно? Разберемся в этом. Если бы было иначе, то временами скорость частицы превысила бы среднюю, а временами была бы ниже ее, а средняя скорость была бы одинаковой, потому что частице надо было бы дойти «отсюда сюда» за условленное время. Например, если тебе нужно попасть из дому в школу на своей машине за определенное время, то сделать это можно по-разному: ты можешь сперва гнать, как сумасшедший, а в кон­це притормозить, или ехать с одинаковой скоростью, или сна­чала можешь даже отправиться в обратную сторону, а уж потом повернуть к школе, и т. д. Во всех случаях средняя скорость, конечно, должна быть одной и той же — частное от деления расстояния от дома до школы на время. Но и при данной сред­ней скорости ты иногда двигался слишком быстро, а иногда чересчур медленно. А средний квадрат чего-то, что отклоняется от среднего, как известно, всегда больше квадрата среднего; значит, интеграл от кинетической энергии при колебаниях скорости движения всегда будет больше, нежели при движении с постоянной скоростью. Ты видишь, что интеграл достигнет минимума, когда скорость будет постоянной (при отсутствии сил). Правильный путь таков.

Предмет же, подброшен­ный в поле тяжести вверх, сперва поднимается быстро, а потом все медленнее. Про­исходит это потому, что он обладает и потенциальной энергией, а наименьшего зна­чения должна достигать раз­ность между кинетической и потенциальной энергиями.

Раз потенциальная энергия возрастает по мере подъема, то меньшая разность получится, если как можно быстрее достичь тех высот, где потенциальная энергия велика. Тогда, вычтя из кинети­ческой энергии этот высокий потенциал, мы добьемся уменьшения среднего. Так что выгоднее такой путь, который идет вверх и постав­ляет добрый отрицательный кусок за счет потенциальной энергии.