Ричард Фейнман - 5a. Электричество и магнетизм

(6.32)

Поля повсюду вне сферы будут получаться наложением полей от q, q'и q ". Задача решена.

Теперь ясно, что между сферой и точечным зарядом q долж­на существовать сила притяжения. Она не пропадает, даже если сфера нейтральна, на ней нет никакого заряда. Откуда же берется притяжение? Когда вы подносите к проводящей сфере положительный заряд, то он притягивает отрицательные за­ряды на ближний конец сферы, положительные же оставляет на дальнем. А притяжение отрицательными зарядами пере­вешивает отталкивание положительными; в итоге остается при­тяжение. Силу его можно прикинуть, подсчитав силу, действую­щую на q в поле, созданном q'и q ". Суммарная сила равна силе притяжения между зарядами q и q' = -(a/b)q на расстоянии b-(а 2/b) плюс сила отталкивания q и заряда q" = + (a/b)q на расстоянии b .

Если вы в детстве любили разглядывать журнал, на облож­ке которого был показан мальчик, разглядывающий журнал, на обложке которого показан мальчик, разглядывающий жур­нал, на обложке которого..., то вас заинтересует и следующая задача. Две одинаковые сферы, одна с зарядом +Q, а другая с зарядом - Q, расположены на некотором расстоянии друг от друга. Какова сила притяжения между ними? Задача решает­ся при помощи бесконечного количества изображений. Первое приближает каждую сферу зарядом в ее центре. Эти заряды создают свои изображения на другой сфере. У изображений в свою очередь есть свои изображения и т. д., и т. д., и т. д. Решение здесь — все равно что картинка на обложке. Схо­дится оно очень быстро.

§ 10. Конденсаторы; параллельные пластины

Теперь обратимся к другому роду задач, связанных с про­водниками. Рассмотрим две широкие металлические пластины, параллельные между собой и разделенные узким (по сравнению с их размерами) промежутком. Предположим, что пластины наэлектризованы равными, но противоположными зарядами.

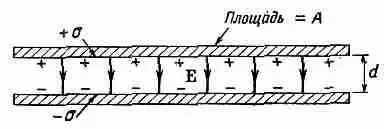
Фиг. 6.12. Плоский конденсатор.

Заряды одной пластины будут притягивать к себе заряды дру­гой и потом равномерно распределятся на внутренней поверх­ности пластин. Пусть поверхностная плотность зарядов на пластинах будет +s и -sсоответственно (фиг. 6.12). Из гл. 5 мы знаем, что поле между пластинами равно s/e 0, а поле снаружи пластин равно нулю. Пластины обладают неравными потен­циалами j 1и j 2. Их разности V удобно дать особое имя, ее часто называют «напряжением»

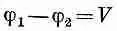
[некоторые обозначают буквой V потенциал, мы же его обозна­чили буквой j].

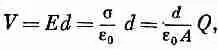
Разность потенциалов V — это работа (на единицу заряда), требуемая для переноса небольшого заряда с одной пластины на другую, так что

(6.33)

где ±Q — суммарный заряд каждой пластины, А — ее пло­щадь, d — щель между пластинами.

Мы видим, что напряжение пропорционально заряду. Эта пропорциональность между V и Q соблюдается для любых двух проводников в пространстве, если на одном из них имеется плюс-заряд, а на другом равный ему минус-заряд. Разность потенциалов между ними, т. е. напряжение, оказывается про­порциональной заряду. (Мы предполагаем, что вокруг нет ни­каких других зарядов.)

Почему возникает эта пропорциональность? Просто из-за принципа наложения. Пусть нам известно решение для одной совокупности зарядов, а потом мы наложим на него другое такое же решение. Заряды удвоятся, поля удвоятся, работа пе­реноса заряда от точки к точке тоже удвоится. По этой причине разность потенциалов двух точек пропорциональна заряду. В частности, разность потенциалов двух проводников пропор­циональна их зарядам. Эту пропорциональность когда-то решили записывать иначе. И стали писать

Q=CV,

где С — постоянное число. Этот коэффициент пропорциональ­ности назвали емкостью, а систему двух проводников — конденсатором. Для нашего конденсатора из параллельных пластин

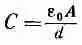
(параллельные обкладки). (6.34)

Эта формула неточна, потому что поле в противоречии с на­шим предположением на самом деле не всюду однородно. Поле не кончается сразу на ребрах пластин, а похоже скорее на то, что изображено на фиг. 6.13. Суммарный заряд тоже равен не sА, как мы предположили; существует маленькая поправ­ка на краевой эффект. Чтобы знать, какова она, надо точнее рас­считать поле и посмотреть, что происходит на краях. Это очень сложная математическая задача, однако ее можно решить при помощи техники, о которой мы, впрочем, говорить здесь не бу­дем. Расчеты показывают, что плотность зарядов возле края пластин слегка возрастает. Это значит, что емкость пластин чуть выше, чем мы думали. [Хорошее приближение для емкости можно получить, если в уравнении (6.34) принять за А площадь, которую имели бы пластины, если б их расширили на 3/ 8расстояния между ними.]

Мы говорили пока только о емкости двух проводников. Иногда люди говорят о емкости предмета самого по себе. Так, говорят, что емкость сферы радиусом а есть 4pe 0 а . При этом подразумевается, что вторым полюсом является сфера беско­нечного радиуса, т. е. что если на сфере помещен заряд

+ Q , то противоположным зарядом - Q обладает бесконечно боль­шая сфера. Можно говорить также о емкостях и тогда, когда проводников три или больше трех, но обсуждение этого во­проса мы отложим до лучших времен.

Пусть нам необходимо иметь конденсатор очень большой емкости. Большую емкость можно получить, взяв очень большую

площадь и очень малый промежуток. Можно про­ложить алюминиевые лен­ты провощенной бумагой и смотать их в трубку. (Поместив ее в пластмас­совую упаковку, мы полу­чим типичный радиоконденсатор.)

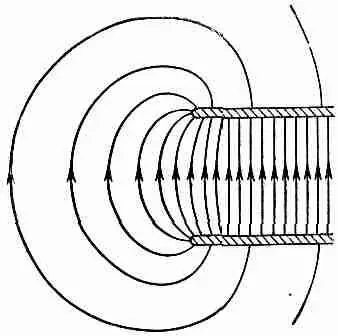
Фиг. 6.13. Электрическое поле у краев двух параллельных пластин.

Зачем они нужны? Они пригодны для того, чтобы накапливать заряд. Если бы мы захотели, например, собрать заряд на каком-то шаре, то его потенциал быстро подско­чил бы, а вскоре так поднялся бы, что заряды стали бы стекать в воздух, и от шара посыпались бы искры. Но если тот же заряд поместить внутрь конденсатора большой емкости, то напряжение близ конденсатора будет очень малым.

Во многих электронных схемах полезно иметь устройство, способное поглощать или выделять большие количества зарядов, заметно не изменяя потенциал. Вот конденсатор (или «емкость»)— как раз такое устройство. Он имеет множество применений и в электронных приборах и в счетных машинах. Там он исполь­зуется для получения определенного изменения в напряжении в ответ на то или иное изменение заряда. С подобным приме­нением мы уже познакомились в вып. 2, гл. 23, когда описыва­ли свойства резонансных контуров.