Ричард Фейнман - 5a. Электричество и магнетизм
- Название:5a. Электричество и магнетизм
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - 5a. Электричество и магнетизм краткое содержание
5a. Электричество и магнетизм - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
где Dr впоследствии надо будет заменить на d/2. Завершая доказательство так, как это было сделано выше, мы приведем уравнение (6.19) к виду
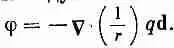
Это то же уравнение, что и (6.16). Надо только заменить qd на р и вставить потерянный по дороге множитель 1/4pe 0. Взглянув на это уравнение по-иному, видим, что дипольный потенциал (6.13) можно толковать как
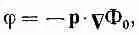
(6.20)
где Ф 0=1/4pe 0r — потенциал единичного точечного заряда.
Хотя потенциал данного распределения зарядов всегда может быть найден при помощи интегрирования, иногда можно сберечь время, применив какой-нибудь хитроумный прием. Например, на помощь часто приходит принцип наложения. Если нам дано распределение зарядов, которое можно составить из двух распределений с уже известными потенциалами, то искомый потенциал легко получить, просто сложив уже известные между собой. Наш вывод формулы (6.20) — один из примеров применения этого приема.
А вот и другой. Пусть имеется сферическая поверхность, на которой поверхностный заряд распределен пропорционально косинусу полярного угла. Интегрировать такое распределение— задача, откровенно говоря, не из приятных. Но как ни странно, на помощь приходит принцип наложения. Представьте себе шар с однородной объемной плотностью положительных зарядов и другой шар с такой же однородной объемной плотностью зарядов, но противоположного знака. Первоначально они вложены друг в друга, образуя нейтральный, т. е. незаряженный шар. Если затем положительный шар чуть сместить по отношению к отрицательному, то нутро незаряженного шара так и останется незаряженным, но на одной стороне возникнет небольшой положительный заряд, а на противоположной — такой же отрицательный (фиг. 6.6). И если относительное смещение двух шаров мало, то эти заряды эквивалентны существованию поверхностного заряда (на сферической поверхности) с плотностью, пропорциональной косинусу полярного угла.
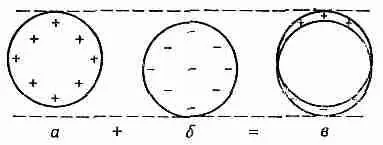
Когда же нам понадобится потенциал этого распределения, то брать интегралы не нужно. Мы знаем, что потенциал каждого заряженного шара —- в точках вне его— совпадает с потенциалом точечного заряда. А два смещенных шара — все равно, что два точечных заряда; значит, искомый потенциал и есть как раз потенциал диполя.
Фиг. 6,6. Две равномерно заряженные сферы, вложенные друг в друга и слегка смещенные, эквивалентны неоднородному распределению
поверхностного заряда.
Таким путем можно показать, что распределение зарядов на сфере радиуса а с поверхностной плотностью

создает снаружи сферы такое же поле, как и диполь с моментом
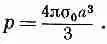
Можно также показать, что внутри сферы поле постоянно и равно
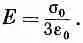
Если q — угол с положительной осью z, то электрическое поле внутри сферы направлено по отрицательной оси z. Рассмотренный нами пример отнюдь не досужая выдумка составителя задач; он нам встретится еще в теории диэлектриков.
§ 5. Дипольное приближение для произвольного распределения
Столь же интересно и не менее важно поле диполя, возникающее при других обстоятельствах. Пусть у нас есть тело со сложным распределением заряда, скажем, как у молекулы воды (см. фиг. 6.2), а нас интересует только поле вдали от него. Мы покажем, что можно получить сравнительно простое выражение для полей, пригодное для расстояний, много больших, чем размеры тела.
Мы можем смотреть на это тело, как на скопление точечных зарядов q i в некоторой ограниченной области (фиг. 6.7). (Позже, если понадобится, мы q i заменим на pdV.) Пускай заряд q i удален от начала координат, выбранного где-то внутри группы зарядов, на расстояние d i . Чему равен потенциал в точке Р, расположенной где-то на отлете, на расстоянии R, много большем, чем самое большое из d i,? Потенциал всего нашего скопления выражается формулой
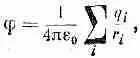
(6.21)
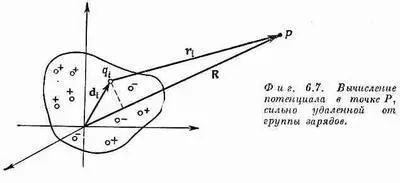
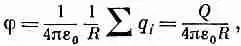
где r i— расстояние от Р до заряда q i (длина вектора R-d i). Если расстояние от зарядов до Р (до точки наблюдения) чрезвычайно велико, то каждое из r iможно принять за R. Каждый член в сумме станет равным q i /R, и 1 IR можно будет вынести из-под знака суммы. Получится простой результат
(6.22)
где Q — суммарный заряд тела. Таким образом, мы убедились, что из точек, достаточно удаленных от скопления зарядов, оно кажется просто точечным зарядом. Этот результат в общем не очень удивителен.
Но что, если положительных и отрицательных зарядов в группе окажется поровну? Суммарный заряд Q тогда будет равен нулю. Это не такой уж редкий случай; мы знаем, что большинство тел нейтрально. Нейтральна молекула воды, но заряды в ней размещаются отнюдь не в одной точке, так что, приблизившись вплотную, мы должны будем заметить какие-то признаки того, что заряды разделены. Для потенциала произвольного распределения зарядов в нейтральном теле мы нуждаемся в приближении, лучшем, чем даваемое формулой (6.22). Уравнение (6.21) по-прежнему годится, но полагать r i =R больше нельзя. Для r iнужно выражение поточнее. В хорошем приближении r iможно считать отличающимся от R (если точка Р сильно удалена) на проекцию вектора d на вектор R (см. фиг. 6.7, но вы должны только представлять себе, что Р намного дальше, чем показано). Иными словами, если e r— единичный вектор в направлении R, то за следующее приближение к r i нужно принять
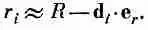
(6.23)
Но нам ведь нужно не r i , а 1/r i; оно в нашем приближении (с учетом d i < равно
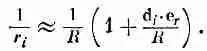
(6.24)
Подставив это в (6.21), мы увидим, что потенциал равен
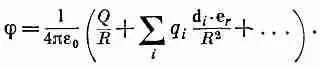
Интервал:
Закладка:





